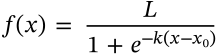Commutative Property of Multiplication
commutative property of multiplication
$$x \cdot y = y \cdot x$$
x \cdot y = y \cdot x
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>x</mi><mi>·</mi><mi>y</mi><mo>=</mo><mi>y</mi><mi>·</mi><mi>x</mi></mrow></math>
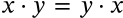
Commutative Property of Addition
commutative property of addition
$$x + y = y + x$$
x + y = y + x
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>x</mi><mo>+</mo><mi>y</mi><mo>=</mo><mi>y</mi><mo>+</mo><mi>x</mi></mrow></math>
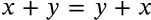
Associative Property of Multiplication
associative property of multiplication
$$(x \cdot y) \cdot z = x \cdot (y \cdot z)$$
(x \cdot y) \cdot z = x \cdot (y \cdot z)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo stretchy="false">(</mo><mi>x</mi><mi>·</mi><mi>y</mi><mo stretchy="false">)</mo><mi>·</mi><mi>z</mi><mo>=</mo><mi>x</mi><mi>·</mi><mo stretchy="false">(</mo><mi>y</mi><mi>·</mi><mi>z</mi><mo stretchy="false">)</mo></mrow></math>
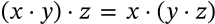
Associative Property of Addition
associative property of addition
$$(x + y) + z = x + (y + z)$$
(x + y) + z = x + (y + z)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo stretchy="false">(</mo><mi>x</mi><mo>+</mo><mi>y</mi><mo stretchy="false">)</mo><mo>+</mo><mi>z</mi><mo>=</mo><mi>x</mi><mo>+</mo><mo stretchy="false">(</mo><mi>y</mi><mo>+</mo><mi>z</mi><mo stretchy="false">)</mo></mrow></math>
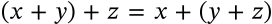
Distributive Property
distributive property
$$x(y+z) = xy + xz$$
x(y+z) = xy + xz
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>x</mi><mo stretchy="false">(</mo><mi>y</mi><mo>+</mo><mi>z</mi><mo stretchy="false">)</mo><mo>=</mo><mi>x</mi><mi>y</mi><mo>+</mo><mi>x</mi><mi>z</mi></mrow></math>
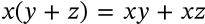
Difference of Two Squares
difference of two squares
$$a^2 - b^2 = (a+b)(a-b)$$
a^2 - b^2 = (a+b)(a-b)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msup><mi>a</mi><mn>2</mn></msup><mo>−</mo><msup><mi>b</mi><mn>2</mn></msup><mo>=</mo><mo stretchy="false">(</mo><mi>a</mi><mo>+</mo><mi>b</mi><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>a</mi><mo>−</mo><mi>b</mi><mo stretchy="false">)</mo></mrow></math>
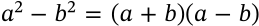
Exponent of One
exponent of one
$$b^1 = b$$
b^1 = b
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msup><mi>b</mi><mn>1</mn></msup><mo>=</mo><mi>b</mi></mrow></math>
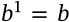
Exponent of Zero
exponent of zero
$$b^0 = 1$$
b^0 = 1
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msup><mi>b</mi><mn>0</mn></msup><mo>=</mo><mn>1</mn></mrow></math>
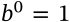
Exponential Sum
exponential sum
$$b^{m+n} = b^m \cdot b^n$$
b^{m+n} = b^m \cdot b^n
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msup><mi>b</mi><mrow><mi>m</mi><mo>+</mo><mi>n</mi></mrow></msup><mo>=</mo><msup><mi>b</mi><mi>m</mi></msup><mi>·</mi><msup><mi>b</mi><mi>n</mi></msup></mrow></math>
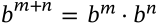
Exponential Product
exponential product
$$(b^m)^n = b^{m \cdot n}$$
(b^m)^n = b^{m \cdot n}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo stretchy="false">(</mo><msup><mi>b</mi><mi>m</mi></msup><msup><mo stretchy="false">)</mo><mi>n</mi></msup><mo>=</mo><msup><mi>b</mi><mrow><mi>m</mi><mi>·</mi><mi>n</mi></mrow></msup></mrow></math>
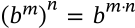
Exponential Product
exponential product
$$(b \cdot c)^n = b^n \cdot c^n$$
(b \cdot c)^n = b^n \cdot c^n
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo stretchy="false">(</mo><mi>b</mi><mi>·</mi><mi>c</mi><msup><mo stretchy="false">)</mo><mi>n</mi></msup><mo>=</mo><msup><mi>b</mi><mi>n</mi></msup><mi>·</mi><msup><mi>c</mi><mi>n</mi></msup></mrow></math>
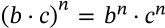
Negative Exponent
negative exponent
$$b^{-m} = \frac{1}{b^m}$$
b^{-m} = \frac{1}{b^m}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msup><mi>b</mi><mrow><mo>−</mo><mi>m</mi></mrow></msup><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><msup><mi>b</mi><mi>m</mi></msup></mrow></mfrac></mrow></math>
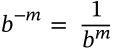
Logarithm of 1
logarithm of 1
$$\log_b(1) = 0$$
\log_b(1) = 0
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msub><mi>log</mi><mi>b</mi></msub><mo stretchy="false">(</mo><mn>1</mn><mo stretchy="false">)</mo><mo>=</mo><mn>0</mn></mrow></math>
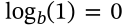
Logarithm of Base
logarithm of base
$$\log_b(b) = 1$$
\log_b(b) = 1
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msub><mi>log</mi><mi>b</mi></msub><mo stretchy="false">(</mo><mi>b</mi><mo stretchy="false">)</mo><mo>=</mo><mn>1</mn></mrow></math>
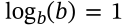
Logarithm Base
logarithm base
$$\log_b(x) = \frac{\log_k(x)}{\log_k(b)}$$
\log_b(x) = \frac{\log_k(x)}{\log_k(b)}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msub><mi>log</mi><mi>b</mi></msub><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><msub><mi>log</mi><mi>k</mi></msub><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo></mrow><mrow><msub><mi>log</mi><mi>k</mi></msub><mo stretchy="false">(</mo><mi>b</mi><mo stretchy="false">)</mo></mrow></mfrac></mrow></math>
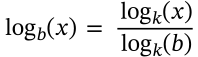
Logarithm Product
logarithm product
$$\log_b(xy) = \log_b(x) + \log_b(y)$$
\log_b(xy) = \log_b(x) + \log_b(y)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msub><mi>log</mi><mi>b</mi></msub><mo stretchy="false">(</mo><mi>x</mi><mi>y</mi><mo stretchy="false">)</mo><mo>=</mo><msub><mi>log</mi><mi>b</mi></msub><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>+</mo><msub><mi>log</mi><mi>b</mi></msub><mo stretchy="false">(</mo><mi>y</mi><mo stretchy="false">)</mo></mrow></math>
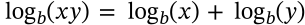
Logarithm Quotient
logarithm quotient
$$\log_b\left(\frac{x}{y}\right) = \log_b(x) - \log_b(y)$$
\log_b\left(\frac{x}{y}\right) = \log_b(x) - \log_b(y)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msub><mi>log</mi><mi>b</mi></msub><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mi>x</mi></mrow><mrow><mi>y</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mo>=</mo><msub><mi>log</mi><mi>b</mi></msub><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>−</mo><msub><mi>log</mi><mi>b</mi></msub><mo stretchy="false">(</mo><mi>y</mi><mo stretchy="false">)</mo></mrow></math>
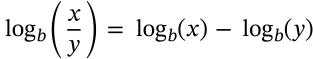
Logarithm of Exponent
logarithm of exponent
$$\log_b(x^p) = p\log_b(x)$$
\log_b(x^p) = p\log_b(x)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msub><mi>log</mi><mi>b</mi></msub><mo stretchy="false">(</mo><msup><mi>x</mi><mi>p</mi></msup><mo stretchy="false">)</mo><mo>=</mo><mi>p</mi><msub><mi>log</mi><mi>b</mi></msub><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo></mrow></math>
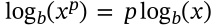
Logarithm Root
logarithm root
$$\log_b(\sqrt[p]{x}) = \frac{\log_b(x)}{p}$$
\log_b(\sqrt[p]{x}) = \frac{\log_b(x)}{p}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msub><mi>log</mi><mi>b</mi></msub><mo stretchy="false">(</mo><mroot><mrow><mi>x</mi></mrow><mi>p</mi></mroot><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><msub><mi>log</mi><mi>b</mi></msub><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo></mrow><mrow><mi>p</mi></mrow></mfrac></mrow></math>
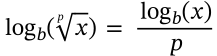
Exponent of Logarithm
exponent of logarithm
$$x^{\log_b(y)} = y^{\log_b(x)}$$
x^{\log_b(y)} = y^{\log_b(x)}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msup><mi>x</mi><mrow><msub><mi>log</mi><mi>b</mi></msub><mo stretchy="false">(</mo><mi>y</mi><mo stretchy="false">)</mo></mrow></msup><mo>=</mo><msup><mi>y</mi><mrow><msub><mi>log</mi><mi>b</mi></msub><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo></mrow></msup></mrow></math>
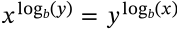
Quadratic Formula
quadratic formula
$$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>x</mi><mo>=</mo><mfrac><mrow><mo>−</mo><mi>b</mi><mi>±</mi><msqrt><mrow><msup><mi>b</mi><mn>2</mn></msup><mo>−</mo><mn>4</mn><mi>a</mi><mi>c</mi></mrow></msqrt></mrow><mrow><mn>2</mn><mi>a</mi></mrow></mfrac></mrow></math>
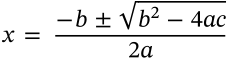
Euler's Identity
euler's identity
$$e^{i\pi} + 1 = 0$$
e^{i\pi} + 1 = 0
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msup><mi>e</mi><mrow><mi>i</mi><mi>π</mi></mrow></msup><mo>+</mo><mn>1</mn><mo>=</mo><mn>0</mn></mrow></math>
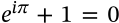
Euler's Formula
euler's formula
$$e^{i \theta} = \cos\theta + i\sin\theta$$
e^{i \theta} = \cos\theta + i\sin\theta
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msup><mi>e</mi><mrow><mi>i</mi><mi>θ</mi></mrow></msup><mo>=</mo><mi>cos</mi><mi>θ</mi><mo>+</mo><mi>i</mi><mi>sin</mi><mi>θ</mi></mrow></math>
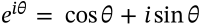
Candido's Identity
candido's identity
$$[x^2 + y^2 + (x+y)^2]^2 = 2[x^4 + y^4 + (x+y)^4]$$
[x^2 + y^2 + (x+y)^2]^2 = 2[x^4 + y^4 + (x+y)^4]
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo stretchy="false">[</mo><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><msup><mi>y</mi><mn>2</mn></msup><mo>+</mo><mo stretchy="false">(</mo><mi>x</mi><mo>+</mo><mi>y</mi><msup><mo stretchy="false">)</mo><mn>2</mn></msup><msup><mo stretchy="false">]</mo><mn>2</mn></msup><mo>=</mo><mn>2</mn><mo stretchy="false">[</mo><msup><mi>x</mi><mn>4</mn></msup><mo>+</mo><msup><mi>y</mi><mn>4</mn></msup><mo>+</mo><mo stretchy="false">(</mo><mi>x</mi><mo>+</mo><mi>y</mi><msup><mo stretchy="false">)</mo><mn>4</mn></msup><mo stretchy="false">]</mo></mrow></math>
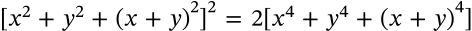
Binomial Identity
binomial identity
$$(x+y)^n = \sum_{k=0}^n \binom{n}{k}n^{n-k}y^k = \sum_{k=0}^n \binom{n}{k}x^k y^{n-k}$$
(x+y)^n = \sum_{k=0}^n \binom{n}{k}n^{n-k}y^k = \sum_{k=0}^n \binom{n}{k}x^k y^{n-k}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo stretchy="false">(</mo><mi>x</mi><mo>+</mo><mi>y</mi><msup><mo stretchy="false">)</mo><mi>n</mi></msup><mo>=</mo><msubsup><mo>∑</mo><mrow><mi>k</mi><mo>=</mo><mn>0</mn></mrow><mi>n</mi></msubsup><mo minsize="2.047em" maxsize="2.047em">(</mo><mfrac linethickness="0"><mrow><mi>n</mi></mrow><mrow><mi>k</mi></mrow></mfrac><mo minsize="2.047em" maxsize="2.047em">)</mo><msup><mi>n</mi><mrow><mi>n</mi><mo>−</mo><mi>k</mi></mrow></msup><msup><mi>y</mi><mi>k</mi></msup><mo>=</mo><msubsup><mo>∑</mo><mrow><mi>k</mi><mo>=</mo><mn>0</mn></mrow><mi>n</mi></msubsup><mo minsize="2.047em" maxsize="2.047em">(</mo><mfrac linethickness="0"><mrow><mi>n</mi></mrow><mrow><mi>k</mi></mrow></mfrac><mo minsize="2.047em" maxsize="2.047em">)</mo><msup><mi>x</mi><mi>k</mi></msup><msup><mi>y</mi><mrow><mi>n</mi><mo>−</mo><mi>k</mi></mrow></msup></mrow></math>
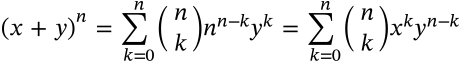
Hermite's Identity
hermite's identity
$$\sum_{k=0}^{n-1} \left\lfloor{x+\frac{k}{n}}\right\rfloor = \lfloor{nx}\rfloor$$
\sum_{k=0}^{n-1} \left\lfloor{x+\frac{k}{n}}\right\rfloor = \lfloor{nx}\rfloor
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msubsup><mo>∑</mo><mrow><mi>k</mi><mo>=</mo><mn>0</mn></mrow><mrow><mi>n</mi><mo>−</mo><mn>1</mn></mrow></msubsup><mrow><mo stretchy="true" fence="true" form="prefix">⌊</mo><mrow><mi>x</mi><mo>+</mo><mfrac><mrow><mi>k</mi></mrow><mrow><mi>n</mi></mrow></mfrac></mrow><mo stretchy="true" fence="true" form="postfix">⌋</mo></mrow><mo>=</mo><mi>⌊</mi><mrow><mi>n</mi><mi>x</mi></mrow><mi>⌋</mi></mrow></math>
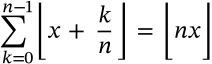
Lagrange's Identity
lagrange's identity
$$\left(\sum_{k=1}^n a_k^2 \right)\left(\sum_{k=1}^n b_k^2\right) - \left(\sum_{k=1}^n a_k b_k\right)^2 = \sum_{i=1}^{n-1}\sum_{j=i+1}^{n}(a_i b_j - a_j b_i)^2$$
\left(\sum_{k=1}^n a_k^2 \right)\left(\sum_{k=1}^n b_k^2\right) - \left(\sum_{k=1}^n a_k b_k\right)^2 = \sum_{i=1}^{n-1}\sum_{j=i+1}^{n}(a_i b_j - a_j b_i)^2
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><msubsup><mo>∑</mo><mrow><mi>k</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></msubsup><msubsup><mi>a</mi><mi>k</mi><mn>2</mn></msubsup><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><msubsup><mo>∑</mo><mrow><mi>k</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></msubsup><msubsup><mi>b</mi><mi>k</mi><mn>2</mn></msubsup><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mo>−</mo><msup><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><msubsup><mo>∑</mo><mrow><mi>k</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></msubsup><msub><mi>a</mi><mi>k</mi></msub><msub><mi>b</mi><mi>k</mi></msub><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mn>2</mn></msup><mo>=</mo><msubsup><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mrow><mi>n</mi><mo>−</mo><mn>1</mn></mrow></msubsup><msubsup><mo>∑</mo><mrow><mi>j</mi><mo>=</mo><mi>i</mi><mo>+</mo><mn>1</mn></mrow><mrow><mi>n</mi></mrow></msubsup><mo stretchy="false">(</mo><msub><mi>a</mi><mi>i</mi></msub><msub><mi>b</mi><mi>j</mi></msub><mo>−</mo><msub><mi>a</mi><mi>j</mi></msub><msub><mi>b</mi><mi>i</mi></msub><msup><mo stretchy="false">)</mo><mn>2</mn></msup></mrow></math>
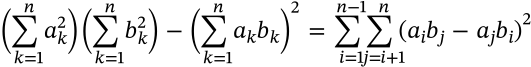
Sun's Curious Identity
sun's curious identity
$$(x+m+1)\sum_{i=0}^m(-1)^i \binom{x+y+i}{m-i}\binom{y+2i}{i} - \sum_{i=0}^m\binom{x+i}{m-i}(-4)^i = (x-m)\binom{x}{m}$$
(x+m+1)\sum_{i=0}^m(-1)^i \binom{x+y+i}{m-i}\binom{y+2i}{i} - \sum_{i=0}^m\binom{x+i}{m-i}(-4)^i = (x-m)\binom{x}{m}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo stretchy="false">(</mo><mi>x</mi><mo>+</mo><mi>m</mi><mo>+</mo><mn>1</mn><mo stretchy="false">)</mo><msubsup><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>0</mn></mrow><mi>m</mi></msubsup><mo stretchy="false">(</mo><mo>−</mo><mn>1</mn><msup><mo stretchy="false">)</mo><mi>i</mi></msup><mo minsize="2.047em" maxsize="2.047em">(</mo><mfrac linethickness="0"><mrow><mi>x</mi><mo>+</mo><mi>y</mi><mo>+</mo><mi>i</mi></mrow><mrow><mi>m</mi><mo>−</mo><mi>i</mi></mrow></mfrac><mo minsize="2.047em" maxsize="2.047em">)</mo><mo minsize="2.047em" maxsize="2.047em">(</mo><mfrac linethickness="0"><mrow><mi>y</mi><mo>+</mo><mn>2</mn><mi>i</mi></mrow><mrow><mi>i</mi></mrow></mfrac><mo minsize="2.047em" maxsize="2.047em">)</mo><mo>−</mo><msubsup><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>0</mn></mrow><mi>m</mi></msubsup><mo minsize="2.047em" maxsize="2.047em">(</mo><mfrac linethickness="0"><mrow><mi>x</mi><mo>+</mo><mi>i</mi></mrow><mrow><mi>m</mi><mo>−</mo><mi>i</mi></mrow></mfrac><mo minsize="2.047em" maxsize="2.047em">)</mo><mo stretchy="false">(</mo><mo>−</mo><mn>4</mn><msup><mo stretchy="false">)</mo><mi>i</mi></msup><mo>=</mo><mo stretchy="false">(</mo><mi>x</mi><mo>−</mo><mi>m</mi><mo stretchy="false">)</mo><mo minsize="2.047em" maxsize="2.047em">(</mo><mfrac linethickness="0"><mrow><mi>x</mi></mrow><mrow><mi>m</mi></mrow></mfrac><mo minsize="2.047em" maxsize="2.047em">)</mo></mrow></math>
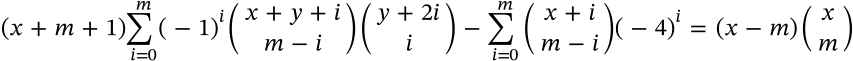
Vandermonde's Identity
vandermonde's identity
$$\binom{m+n}{r} = \sum_{k=0}^r \binom{m}{k} \binom{n}{r-k}$$
\binom{m+n}{r} = \sum_{k=0}^r \binom{m}{k} \binom{n}{r-k}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo minsize="2.047em" maxsize="2.047em">(</mo><mfrac linethickness="0"><mrow><mi>m</mi><mo>+</mo><mi>n</mi></mrow><mrow><mi>r</mi></mrow></mfrac><mo minsize="2.047em" maxsize="2.047em">)</mo><mo>=</mo><msubsup><mo>∑</mo><mrow><mi>k</mi><mo>=</mo><mn>0</mn></mrow><mi>r</mi></msubsup><mo minsize="2.047em" maxsize="2.047em">(</mo><mfrac linethickness="0"><mrow><mi>m</mi></mrow><mrow><mi>k</mi></mrow></mfrac><mo minsize="2.047em" maxsize="2.047em">)</mo><mo minsize="2.047em" maxsize="2.047em">(</mo><mfrac linethickness="0"><mrow><mi>n</mi></mrow><mrow><mi>r</mi><mo>−</mo><mi>k</mi></mrow></mfrac><mo minsize="2.047em" maxsize="2.047em">)</mo></mrow></math>
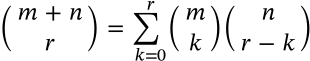
Golden Ratio
golden ratio
$$\varphi = \frac{1 + \sqrt{5}}{2}$$
\varphi = \frac{1 + \sqrt{5}}{2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>φ</mi><mo>=</mo><mfrac><mrow><mn>1</mn><mo>+</mo><msqrt><mrow><mn>5</mn></mrow></msqrt></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>
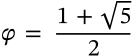
Supergolden Ratio
supergolden ratio
$$\psi = \frac{1 + \sqrt[3]{\frac{29+3\sqrt{93}}{2}} + \sqrt[3]{\frac{29-3\sqrt{93}}{2}}}{3}$$
\psi = \frac{1 + \sqrt[3]{\frac{29+3\sqrt{93}}{2}} + \sqrt[3]{\frac{29-3\sqrt{93}}{2}}}{3}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>ψ</mi><mo>=</mo><mfrac><mrow><mn>1</mn><mo>+</mo><mroot><mrow><mfrac><mrow><mn>29</mn><mo>+</mo><mn>3</mn><msqrt><mrow><mn>93</mn></mrow></msqrt></mrow><mrow><mn>2</mn></mrow></mfrac></mrow><mn>3</mn></mroot><mo>+</mo><mroot><mrow><mfrac><mrow><mn>29</mn><mo>−</mo><mn>3</mn><msqrt><mrow><mn>93</mn></mrow></msqrt></mrow><mrow><mn>2</mn></mrow></mfrac></mrow><mn>3</mn></mroot></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math>
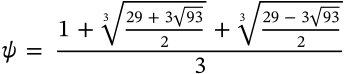
Silver Ratio
silver ratio
$$1 + \sqrt{2}$$
1 + \sqrt{2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mn>1</mn><mo>+</mo><msqrt><mrow><mn>2</mn></mrow></msqrt></mrow></math>
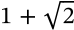
Bronze Ratio
bronze ratio
$$\frac{3 + \sqrt{13}}{2}$$
\frac{3 + \sqrt{13}}{2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mfrac><mrow><mn>3</mn><mo>+</mo><msqrt><mrow><mn>13</mn></mrow></msqrt></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>
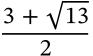
Plastic Number
plastic number
$$\rho = \sqrt[3]{\frac{9 + \sqrt{69}}{18}} + \sqrt[3]{\frac{9 - \sqrt{69}}{18}}$$
\rho = \sqrt[3]{\frac{9 + \sqrt{69}}{18}} + \sqrt[3]{\frac{9 - \sqrt{69}}{18}}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>ρ</mi><mo>=</mo><mroot><mrow><mfrac><mrow><mn>9</mn><mo>+</mo><msqrt><mrow><mn>69</mn></mrow></msqrt></mrow><mrow><mn>18</mn></mrow></mfrac></mrow><mn>3</mn></mroot><mo>+</mo><mroot><mrow><mfrac><mrow><mn>9</mn><mo>−</mo><msqrt><mrow><mn>69</mn></mrow></msqrt></mrow><mrow><mn>18</mn></mrow></mfrac></mrow><mn>3</mn></mroot></mrow></math>
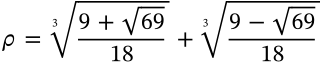
Matrix Determinant Lemma
matrix determinant lemma
$$\mathrm{\det}(\mathbf{A} + \mathbf{uv}^\intercal) = (1 + \bf{v}^\intercal \mathbf{A}^{-1} \bf{u}) \mathbf{A}$$
\mathrm{\det}(\mathbf{A} + \mathbf{uv}^\intercal) = (1 + \bf{v}^\intercal \mathbf{A}^{-1} \bf{u}) \mathbf{A}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mrow><mo movablelimits="true">det</mo></mrow><mo stretchy="false">(</mo><mi>𝐀</mi><mo>+</mo><msup><mrow><mi mathvariant="bold">u</mi><mi mathvariant="bold">v</mi></mrow><mo>⊺</mo></msup><mo stretchy="false">)</mo><mo>=</mo><mo stretchy="false">(</mo><mn>1</mn><mo>+</mo><msup><mrow><mi mathvariant="bold">v</mi></mrow><mo>⊺</mo></msup><msup><mi mathvariant="bold">𝐀</mi><mrow><mo>−</mo><mn>1</mn></mrow></msup><mrow><mi mathvariant="bold">u</mi></mrow><mo stretchy="false">)</mo><mi mathvariant="bold">𝐀</mi></mrow></math>
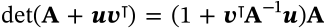
Pythagorean Identity
pythagorean identity trigonometry
$$\sin^2 \theta + \cos^2 \theta = 1$$
\sin^2 \theta + \cos^2 \theta = 1
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msup><mi>sin</mi><mn>2</mn></msup><mi>θ</mi><mo>+</mo><msup><mi>cos</mi><mn>2</mn></msup><mi>θ</mi><mo>=</mo><mn>1</mn></mrow></math>
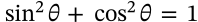
Pythagorean Identity
pythagorean identity trigonometry
$$\tan^2 \theta + 1 = \sec^2 \theta$$
\tan^2 \theta + 1 = \sec^2 \theta
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msup><mi>tan</mi><mn>2</mn></msup><mi>θ</mi><mo>+</mo><mn>1</mn><mo>=</mo><msup><mi>sec</mi><mn>2</mn></msup><mi>θ</mi></mrow></math>
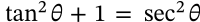
Pythagorean Identity
pythagorean identity trigonometry
$$1 + \cot^2 \theta = \csc^2 \theta$$
1 + \cot^2 \theta = \csc^2 \theta
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mn>1</mn><mo>+</mo><msup><mi>cot</mi><mn>2</mn></msup><mi>θ</mi><mo>=</mo><msup><mi>csc</mi><mn>2</mn></msup><mi>θ</mi></mrow></math>
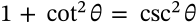
Tangent Definition
tangent definition trigonometry
$$\tan \theta = \frac{\sin \theta}{\cos \theta}$$
\tan \theta = \frac{\sin \theta}{\cos \theta}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>tan</mi><mi>θ</mi><mo>=</mo><mfrac><mrow><mi>sin</mi><mi>θ</mi></mrow><mrow><mi>cos</mi><mi>θ</mi></mrow></mfrac></mrow></math>
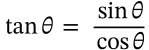
Ptolemy's Sine Identity
ptolemy's sine identity trigonometry
$$\sin(\alpha \pm \beta) = \sin\alpha\cos\beta \pm \cos\alpha \sin\beta$$
\sin(\alpha \pm \beta) = \sin\alpha\cos\beta \pm \cos\alpha \sin\beta
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>sin</mi><mo stretchy="false">(</mo><mi>α</mi><mi>±</mi><mi>β</mi><mo stretchy="false">)</mo><mo>=</mo><mi>sin</mi><mi>α</mi><mi>cos</mi><mi>β</mi><mi>±</mi><mi>cos</mi><mi>α</mi><mi>sin</mi><mi>β</mi></mrow></math>
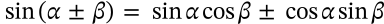
Ptolemy's Cosine Identity
ptolemy's cosine identity trigonometry
$$\cos(\alpha \pm \beta) = \cos\alpha\cos\beta \mp \sin\alpha \sin\beta$$
\cos(\alpha \pm \beta) = \cos\alpha\cos\beta \mp \sin\alpha \sin\beta
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>cos</mi><mo stretchy="false">(</mo><mi>α</mi><mi>±</mi><mi>β</mi><mo stretchy="false">)</mo><mo>=</mo><mi>cos</mi><mi>α</mi><mi>cos</mi><mi>β</mi><mo>∓</mo><mi>sin</mi><mi>α</mi><mi>sin</mi><mi>β</mi></mrow></math>
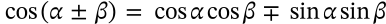
Tangent Identity
tangent identity trigonometry
$$\tan(\alpha \pm \beta) = \frac{\tan\alpha \pm \tan\beta}{1 \mp \tan\alpha\tan\beta}$$
\tan(\alpha \pm \beta) = \frac{\tan\alpha \pm \tan\beta}{1 \mp \tan\alpha\tan\beta}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>tan</mi><mo stretchy="false">(</mo><mi>α</mi><mi>±</mi><mi>β</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mi>tan</mi><mi>α</mi><mi>±</mi><mi>tan</mi><mi>β</mi></mrow><mrow><mn>1</mn><mo>∓</mo><mi>tan</mi><mi>α</mi><mi>tan</mi><mi>β</mi></mrow></mfrac></mrow></math>
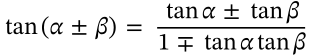
Double Angle Identity (Sine)
double angle identity (sine) trigonometry
$$\sin(2\theta) = 2\sin\theta\cos\theta$$
\sin(2\theta) = 2\sin\theta\cos\theta
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>sin</mi><mo stretchy="false">(</mo><mn>2</mn><mi>θ</mi><mo stretchy="false">)</mo><mo>=</mo><mn>2</mn><mi>sin</mi><mi>θ</mi><mi>cos</mi><mi>θ</mi></mrow></math>
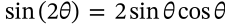
Double Angle Identity (Cosine)
double angle identity (cosine) trigonometry
$$\cos(2\theta) = \cos^2\theta - \sin^2\theta = 2\cos^2\theta - 1 = 1 - 2 \sin^2 \theta$$
\cos(2\theta) = \cos^2\theta - \sin^2\theta = 2\cos^2\theta - 1 = 1 - 2 \sin^2 \theta
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>cos</mi><mo stretchy="false">(</mo><mn>2</mn><mi>θ</mi><mo stretchy="false">)</mo><mo>=</mo><msup><mi>cos</mi><mn>2</mn></msup><mi>θ</mi><mo>−</mo><msup><mi>sin</mi><mn>2</mn></msup><mi>θ</mi><mo>=</mo><mn>2</mn><msup><mi>cos</mi><mn>2</mn></msup><mi>θ</mi><mo>−</mo><mn>1</mn><mo>=</mo><mn>1</mn><mo>−</mo><mn>2</mn><msup><mi>sin</mi><mn>2</mn></msup><mi>θ</mi></mrow></math>
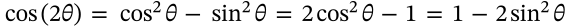
Double Angle Identity (Tangent)
double angle identity (tangent) trigonometry
$$\tan(2\theta) = \frac{2 \tan \theta}{1 - \tan^2 \theta}$$
\tan(2\theta) = \frac{2 \tan \theta}{1 - \tan^2 \theta}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>tan</mi><mo stretchy="false">(</mo><mn>2</mn><mi>θ</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mn>2</mn><mi>tan</mi><mi>θ</mi></mrow><mrow><mn>1</mn><mo>−</mo><msup><mi>tan</mi><mn>2</mn></msup><mi>θ</mi></mrow></mfrac></mrow></math>
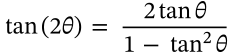
Negative Sine Identity
negative sine identity trigonometry
$$\sin(-\theta) = -\sin\theta$$
\sin(-\theta) = -\sin\theta
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>sin</mi><mo stretchy="false">(</mo><mo>−</mo><mi>θ</mi><mo stretchy="false">)</mo><mo>=</mo><mo>−</mo><mi>sin</mi><mi>θ</mi></mrow></math>
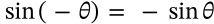
Negative Cosine Identity
negative cosine identity trigonometry
$$\cos(-\theta) = \cos\theta$$
\cos(-\theta) = \cos\theta
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>cos</mi><mo stretchy="false">(</mo><mo>−</mo><mi>θ</mi><mo stretchy="false">)</mo><mo>=</mo><mi>cos</mi><mi>θ</mi></mrow></math>
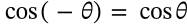
Negative Tangent Identity
negative tangent identity trigonometry
$$\tan(-\theta) = -\tan\theta$$
\tan(-\theta) = -\tan\theta
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>tan</mi><mo stretchy="false">(</mo><mo>−</mo><mi>θ</mi><mo stretchy="false">)</mo><mo>=</mo><mo>−</mo><mi>tan</mi><mi>θ</mi></mrow></math>
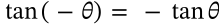
Half Angle Identity (Sine)
half angle identity (sine) trigonometry
$$\sin\frac{\theta}{2} = \pm \sqrt{\frac{1-\cos\theta}{2}}$$
\sin\frac{\theta}{2} = \pm \sqrt{\frac{1-\cos\theta}{2}}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>sin</mi><mfrac><mrow><mi>θ</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mo>=</mo><mi>±</mi><msqrt><mrow><mfrac><mrow><mn>1</mn><mo>−</mo><mi>cos</mi><mi>θ</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></msqrt></mrow></math>
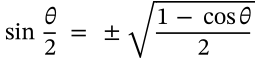
Half Angle Identity (Cosine)
half angle identity (cosine) trigonometry
$$\cos\frac{\theta}{2} = \pm \sqrt{\frac{1+\cos\theta}{2}}$$
\cos\frac{\theta}{2} = \pm \sqrt{\frac{1+\cos\theta}{2}}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>cos</mi><mfrac><mrow><mi>θ</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mo>=</mo><mi>±</mi><msqrt><mrow><mfrac><mrow><mn>1</mn><mo>+</mo><mi>cos</mi><mi>θ</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></msqrt></mrow></math>
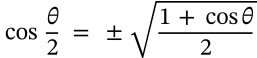
Half Angle Identity (Tangent)
half angle identity (tangent) trigonometry
$$\tan\frac{\theta}{2} = \frac{\sin\theta}{1+\cos\theta} = \frac{1-\cos\theta}{\sin\theta}$$
\tan\frac{\theta}{2} = \frac{\sin\theta}{1+\cos\theta} = \frac{1-\cos\theta}{\sin\theta}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>tan</mi><mfrac><mrow><mi>θ</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mo>=</mo><mfrac><mrow><mi>sin</mi><mi>θ</mi></mrow><mrow><mn>1</mn><mo>+</mo><mi>cos</mi><mi>θ</mi></mrow></mfrac><mo>=</mo><mfrac><mrow><mn>1</mn><mo>−</mo><mi>cos</mi><mi>θ</mi></mrow><mrow><mi>sin</mi><mi>θ</mi></mrow></mfrac></mrow></math>
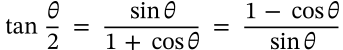
Sine Product-Sum Identity
sine product-sum identity
$$\sin \alpha + \sin \beta = 2\sin\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}$$
\sin \alpha + \sin \beta = 2\sin\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>sin</mi><mi>α</mi><mo>+</mo><mi>sin</mi><mi>β</mi><mo>=</mo><mn>2</mn><mi>sin</mi><mfrac><mrow><mi>α</mi><mo>+</mo><mi>β</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mi>cos</mi><mfrac><mrow><mi>α</mi><mo>−</mo><mi>β</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>
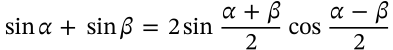
Sine Product-Sum Identity
sine product-sum identity
$$\sin \alpha - \sin \beta = 2\cos\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}$$
\sin \alpha - \sin \beta = 2\cos\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>sin</mi><mi>α</mi><mo>−</mo><mi>sin</mi><mi>β</mi><mo>=</mo><mn>2</mn><mi>cos</mi><mfrac><mrow><mi>α</mi><mo>+</mo><mi>β</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mi>sin</mi><mfrac><mrow><mi>α</mi><mo>−</mo><mi>β</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>
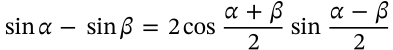
Cosine Product-Sum Identity
cosine product-sum identity
$$\cos \alpha + \cos \beta = 2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}$$
\cos \alpha + \cos \beta = 2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>cos</mi><mi>α</mi><mo>+</mo><mi>cos</mi><mi>β</mi><mo>=</mo><mn>2</mn><mi>cos</mi><mfrac><mrow><mi>α</mi><mo>+</mo><mi>β</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mi>cos</mi><mfrac><mrow><mi>α</mi><mo>−</mo><mi>β</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>
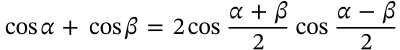
Cosine Product-Sum Identity
cosine product-sum identity
$$\cos \alpha - \cos \beta = -2\sin\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}$$
\cos \alpha - \cos \beta = -2\sin\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>cos</mi><mi>α</mi><mo>−</mo><mi>cos</mi><mi>β</mi><mo>=</mo><mo>−</mo><mn>2</mn><mi>sin</mi><mfrac><mrow><mi>α</mi><mo>+</mo><mi>β</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mi>sin</mi><mfrac><mrow><mi>α</mi><mo>−</mo><mi>β</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>
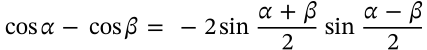
Sine Cosine Product Identity
sine cosine product identity
$$\sin\alpha \cos\beta = \frac{\sin(\alpha+\beta)+\sin(\alpha-\beta)}{2}$$
\sin\alpha \cos\beta = \frac{\sin(\alpha+\beta)+\sin(\alpha-\beta)}{2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>sin</mi><mi>α</mi><mi>cos</mi><mi>β</mi><mo>=</mo><mfrac><mrow><mi>sin</mi><mo stretchy="false">(</mo><mi>α</mi><mo>+</mo><mi>β</mi><mo stretchy="false">)</mo><mo>+</mo><mi>sin</mi><mo stretchy="false">(</mo><mi>α</mi><mo>−</mo><mi>β</mi><mo stretchy="false">)</mo></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>
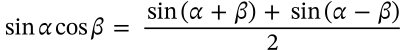
Sine Sine Product Identity
sine sine product identity
$$\sin\alpha \sin\beta = \frac{\cos(\alpha-\beta)-\cos(\alpha+\beta)}{2}$$
\sin\alpha \sin\beta = \frac{\cos(\alpha-\beta)-\cos(\alpha+\beta)}{2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>sin</mi><mi>α</mi><mi>sin</mi><mi>β</mi><mo>=</mo><mfrac><mrow><mi>cos</mi><mo stretchy="false">(</mo><mi>α</mi><mo>−</mo><mi>β</mi><mo stretchy="false">)</mo><mo>−</mo><mi>cos</mi><mo stretchy="false">(</mo><mi>α</mi><mo>+</mo><mi>β</mi><mo stretchy="false">)</mo></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>
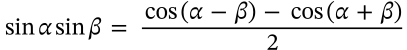
Cosine Cosine Product Identity
cosine cosine product identity
$$\cos\alpha \cos\beta = \frac{\cos(\alpha+\beta)+\cos(\alpha-\beta)}{2}$$
\cos\alpha \cos\beta = \frac{\cos(\alpha+\beta)+\cos(\alpha-\beta)}{2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>cos</mi><mi>α</mi><mi>cos</mi><mi>β</mi><mo>=</mo><mfrac><mrow><mi>cos</mi><mo stretchy="false">(</mo><mi>α</mi><mo>+</mo><mi>β</mi><mo stretchy="false">)</mo><mo>+</mo><mi>cos</mi><mo stretchy="false">(</mo><mi>α</mi><mo>−</mo><mi>β</mi><mo stretchy="false">)</mo></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>
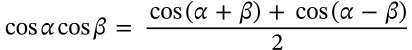
Pythagorean Theorem
pythagorean theorem triangle trigonometry
$$c^2 = a^2 + b^2$$
c^2 = a^2 + b^2
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msup><mi>c</mi><mn>2</mn></msup><mo>=</mo><msup><mi>a</mi><mn>2</mn></msup><mo>+</mo><msup><mi>b</mi><mn>2</mn></msup></mrow></math>
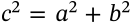
Law of Sines
law of sines angle triangle
$$\frac{\sin A}{a} = \frac{\sin B}{b} \frac{\sin C}{c}$$
\frac{\sin A}{a} = \frac{\sin B}{b} \frac{\sin C}{c}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mfrac><mrow><mi>sin</mi><mi>A</mi></mrow><mrow><mi>a</mi></mrow></mfrac><mo>=</mo><mfrac><mrow><mi>sin</mi><mi>B</mi></mrow><mrow><mi>b</mi></mrow></mfrac><mfrac><mrow><mi>sin</mi><mi>C</mi></mrow><mrow><mi>c</mi></mrow></mfrac></mrow></math>
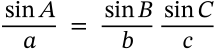
Law of Cosines
law of cosines angle triangle trigonometry
$$c = \sqrt{a^2 + b^2 - 2ab \cos(\theta)}$$
c = \sqrt{a^2 + b^2 - 2ab \cos(\theta)}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>c</mi><mo>=</mo><msqrt><mrow><msup><mi>a</mi><mn>2</mn></msup><mo>+</mo><msup><mi>b</mi><mn>2</mn></msup><mo>−</mo><mn>2</mn><mi>a</mi><mi>b</mi><mi>cos</mi><mo stretchy="false">(</mo><mi>θ</mi><mo stretchy="false">)</mo></mrow></msqrt></mrow></math>
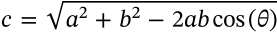
Law of Tangents
law of tangents angle triangle
$$\frac{a-b}{a+b} = \frac{\tan \frac{1}{2}(\alpha-\beta)}{\tan \frac{1}{2}(\alpha+\beta)}$$
\frac{a-b}{a+b} = \frac{\tan \frac{1}{2}(\alpha-\beta)}{\tan \frac{1}{2}(\alpha+\beta)}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mfrac><mrow><mi>a</mi><mo>−</mo><mi>b</mi></mrow><mrow><mi>a</mi><mo>+</mo><mi>b</mi></mrow></mfrac><mo>=</mo><mfrac><mrow><mi>tan</mi><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mo stretchy="false">(</mo><mi>α</mi><mo>−</mo><mi>β</mi><mo stretchy="false">)</mo></mrow><mrow><mi>tan</mi><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mo stretchy="false">(</mo><mi>α</mi><mo>+</mo><mi>β</mi><mo stretchy="false">)</mo></mrow></mfrac></mrow></math>
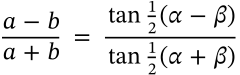
Mollweide's Formula
mollweide's formula
$$\frac{a+b}{c} = \frac{\cos\left(\frac{\alpha-\beta}{2}\right)}{\sin\left(\frac{\gamma}{2}\right)}$$
\frac{a+b}{c} = \frac{\cos\left(\frac{\alpha-\beta}{2}\right)}{\sin\left(\frac{\gamma}{2}\right)}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mfrac><mrow><mi>a</mi><mo>+</mo><mi>b</mi></mrow><mrow><mi>c</mi></mrow></mfrac><mo>=</mo><mfrac><mrow><mi>cos</mi><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mi>α</mi><mo>−</mo><mi>β</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow></mrow><mrow><mi>sin</mi><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mi>γ</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow></mrow></mfrac></mrow></math>
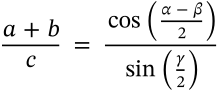
Arc Length
arc length
$$s = r \theta$$
s = r \theta
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>s</mi><mo>=</mo><mi>r</mi><mi>θ</mi></mrow></math>
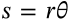
Area of a Triangle
area of a triangle
$$A = \frac{1}{2}bh$$
A = \frac{1}{2}bh
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>A</mi><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mi>b</mi><mi>h</mi></mrow></math>
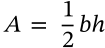
Area of a Circle
area of a circle
$$A = \pi r^2$$
A = \pi r^2
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>A</mi><mo>=</mo><mi>π</mi><msup><mi>r</mi><mn>2</mn></msup></mrow></math>
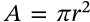
Area of an Ellipse
area of an ellipse
$$A = \pi a b$$
A = \pi a b
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>A</mi><mo>=</mo><mi>π</mi><mi>a</mi><mi>b</mi></mrow></math>
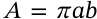
Circumference of a Circle
circumference of a circle
$$C = 2 \pi r$$
C = 2 \pi r
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>C</mi><mo>=</mo><mn>2</mn><mi>π</mi><mi>r</mi></mrow></math>
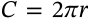
Volume of a Sphere
volume of a sphere
$$V = \frac{4}{3} \pi r^3$$
V = \frac{4}{3} \pi r^3
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>V</mi><mo>=</mo><mfrac><mrow><mn>4</mn></mrow><mrow><mn>3</mn></mrow></mfrac><mi>π</mi><msup><mi>r</mi><mn>3</mn></msup></mrow></math>
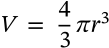
Volume of a Cone
volume of a cone
$$V = \pi r^2 \frac{h}{3}$$
V = \pi r^2 \frac{h}{3}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>V</mi><mo>=</mo><mi>π</mi><msup><mi>r</mi><mn>2</mn></msup><mfrac><mrow><mi>h</mi></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math>
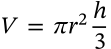
Volume of a Torus
volume of a torus
$$V = (\pi r^2)(2 \pi R)$$
V = (\pi r^2)(2 \pi R)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>V</mi><mo>=</mo><mo stretchy="false">(</mo><mi>π</mi><msup><mi>r</mi><mn>2</mn></msup><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mn>2</mn><mi>π</mi><mi>R</mi><mo stretchy="false">)</mo></mrow></math>
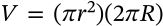
Volume of a Tetrahedron
volume of a tetrahedron platonic solid
$$V = \frac{a^3}{6\sqrt{2}}$$
V = \frac{a^3}{6\sqrt{2}}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>V</mi><mo>=</mo><mfrac><mrow><msup><mi>a</mi><mn>3</mn></msup></mrow><mrow><mn>6</mn><msqrt><mrow><mn>2</mn></mrow></msqrt></mrow></mfrac></mrow></math>
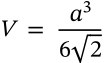
Volume of a Cube
volume of a cube platonic solid
$$V = a^3$$
V = a^3
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>V</mi><mo>=</mo><msup><mi>a</mi><mn>3</mn></msup></mrow></math>
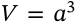
Volume of an Octahedron
volume of an octahedron platonic solid
$$V = \frac{\sqrt{2}}{3} a^3$$
V = \frac{\sqrt{2}}{3} a^3
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>V</mi><mo>=</mo><mfrac><mrow><msqrt><mrow><mn>2</mn></mrow></msqrt></mrow><mrow><mn>3</mn></mrow></mfrac><msup><mi>a</mi><mn>3</mn></msup></mrow></math>
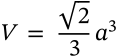
Volume of a Dodecahedron
volume of a dodecahedron platonic solid
$$V = \frac{1}{4}(15 + 7\sqrt{5}) a^3$$
V = \frac{1}{4}(15 + 7\sqrt{5}) a^3
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>V</mi><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>4</mn></mrow></mfrac><mo stretchy="false">(</mo><mn>15</mn><mo>+</mo><mn>7</mn><msqrt><mrow><mn>5</mn></mrow></msqrt><mo stretchy="false">)</mo><msup><mi>a</mi><mn>3</mn></msup></mrow></math>
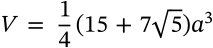
Volume of an Icasohedron
volume of an icasohedron platonic solid
$$V = \frac{5}{3 + \sqrt{5}}{12} a^3$$
V = \frac{5}{3 + \sqrt{5}}{12} a^3
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>V</mi><mo>=</mo><mfrac><mrow><mn>5</mn></mrow><mrow><mn>3</mn><mo>+</mo><msqrt><mrow><mn>5</mn></mrow></msqrt></mrow></mfrac><mrow><mn>12</mn></mrow><msup><mi>a</mi><mn>3</mn></msup></mrow></math>
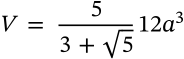
Surface Area of a Sphere
surface area of a sphere
$$A = 4 \pi r^2$$
A = 4 \pi r^2
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>A</mi><mo>=</mo><mn>4</mn><mi>π</mi><msup><mi>r</mi><mn>2</mn></msup></mrow></math>
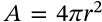
Surface Area of a Cone
surface area of a cone
$$A = \pi r(r + \sqrt{h^2 + r^2})$$
A = \pi r(r + \sqrt{h^2 + r^2})
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>A</mi><mo>=</mo><mi>π</mi><mi>r</mi><mo stretchy="false">(</mo><mi>r</mi><mo>+</mo><msqrt><mrow><msup><mi>h</mi><mn>2</mn></msup><mo>+</mo><msup><mi>r</mi><mn>2</mn></msup></mrow></msqrt><mo stretchy="false">)</mo></mrow></math>
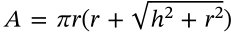
Surface Area of a Torus
surface area of a torus
$$A = (2 \pi R)(2 \pi r)$$
A = (2 \pi R)(2 \pi r)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>A</mi><mo>=</mo><mo stretchy="false">(</mo><mn>2</mn><mi>π</mi><mi>R</mi><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mn>2</mn><mi>π</mi><mi>r</mi><mo stretchy="false">)</mo></mrow></math>
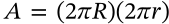
Surface Area of a Tetrahedron
surface area of a tetrahedron platonic solid
$$A = \sqrt{3} a^2$$
A = \sqrt{3} a^2
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>A</mi><mo>=</mo><msqrt><mrow><mn>3</mn></mrow></msqrt><msup><mi>a</mi><mn>2</mn></msup></mrow></math>
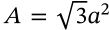
Surface Area of a Cube
surface area of a cube platonic solid
$$A = 6a^2$$
A = 6a^2
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>A</mi><mo>=</mo><mn>6</mn><msup><mi>a</mi><mn>2</mn></msup></mrow></math>
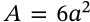
Surface Area of an Octahedron
surface area of an octahedron platonic solid
$$A = 2\sqrt{3} a^2$$
A = 2\sqrt{3} a^2
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>A</mi><mo>=</mo><mn>2</mn><msqrt><mrow><mn>3</mn></mrow></msqrt><msup><mi>a</mi><mn>2</mn></msup></mrow></math>
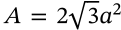
Surface Area of a Dodecahedron
surface area of a dodecahedron platonic solid
$$A = 3\sqrt{25 + 10\sqrt{5}} a^2$$
A = 3\sqrt{25 + 10\sqrt{5}} a^2
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>A</mi><mo>=</mo><mn>3</mn><msqrt><mrow><mn>25</mn><mo>+</mo><mn>10</mn><msqrt><mrow><mn>5</mn></mrow></msqrt></mrow></msqrt><msup><mi>a</mi><mn>2</mn></msup></mrow></math>
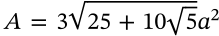
Surface Area of an Icosahedron
surface area of an icosahedron platonic solid
$$A = 5\sqrt{3} a^2$$
A = 5\sqrt{3} a^2
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>A</mi><mo>=</mo><mn>5</mn><msqrt><mrow><mn>3</mn></mrow></msqrt><msup><mi>a</mi><mn>2</mn></msup></mrow></math>
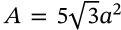
Height of a Tetrahedron
height of a tetrahedron platonic solid
$$\sqrt{\frac{2}{3}} a$$
\sqrt{\frac{2}{3}} a
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msqrt><mrow><mfrac><mrow><mn>2</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></msqrt><mi>a</mi></mrow></math>
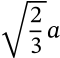
Cylindrical to Cartesian Coordinates
cylindrical to cartesian coordinates
$$ \begin{matrix} x = \rho \, \cos{\varphi} \\ y = \rho \, \sin{\varphi} \\ z = z \end{matrix} $$
\begin{matrix}
x = \rho \, \cos{\varphi} \\
y = \rho \, \sin{\varphi} \\
z = z
\end{matrix}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mtable><mtr><mtd><mi>x</mi><mo>=</mo><mi>ρ</mi><mspace width="0.167em" /><mi>cos</mi><mrow><mi>φ</mi></mrow></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mi>ρ</mi><mspace width="0.167em" /><mi>sin</mi><mrow><mi>φ</mi></mrow></mtd></mtr><mtr><mtd><mi>z</mi><mo>=</mo><mi>z</mi></mtd></mtr></mtable></mrow></math>
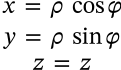
Cartesian to Cylindrical Coordinates
cartesian to cylindrical coordinates
$$ \begin{matrix} \rho = \sqrt{x^2 + y^2} \\ \phi = \tan^{-1}(y/x) \\ z = z \end{matrix} $$
\begin{matrix}
\rho = \sqrt{x^2 + y^2} \\
\phi = \tan^{-1}(y/x) \\
z = z
\end{matrix}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mtable><mtr><mtd><mi>ρ</mi><mo>=</mo><msqrt><mrow><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><msup><mi>y</mi><mn>2</mn></msup></mrow></msqrt></mtd></mtr><mtr><mtd><mi>ϕ</mi><mo>=</mo><msup><mi>tan</mi><mrow><mo>−</mo><mn>1</mn></mrow></msup><mo stretchy="false">(</mo><mi>y</mi><mo>/</mo><mi>x</mi><mo stretchy="false">)</mo></mtd></mtr><mtr><mtd><mi>z</mi><mo>=</mo><mi>z</mi></mtd></mtr></mtable></mrow></math>
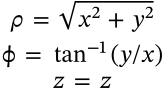
Cartesian to Spherical Coordinates
cartesian to spherical coordinates
$$\begin{matrix} r = \sqrt{x^2 + y^2 + z^2}\\ \theta = \cos^{-1}(z/r)\\ \varphi = \tan^{-1}(y/x) \end{matrix} $$
\begin{matrix}
r = \sqrt{x^2 + y^2 + z^2}\\
\theta = \cos^{-1}(z/r)\\
\varphi = \tan^{-1}(y/x)
\end{matrix}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mtable><mtr><mtd><mi>r</mi><mo>=</mo><msqrt><mrow><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><msup><mi>y</mi><mn>2</mn></msup><mo>+</mo><msup><mi>z</mi><mn>2</mn></msup></mrow></msqrt></mtd></mtr><mtr><mtd><mi>θ</mi><mo>=</mo><msup><mi>cos</mi><mrow><mo>−</mo><mn>1</mn></mrow></msup><mo stretchy="false">(</mo><mi>z</mi><mo>/</mo><mi>r</mi><mo stretchy="false">)</mo></mtd></mtr><mtr><mtd><mi>φ</mi><mo>=</mo><msup><mi>tan</mi><mrow><mo>−</mo><mn>1</mn></mrow></msup><mo stretchy="false">(</mo><mi>y</mi><mo>/</mo><mi>x</mi><mo stretchy="false">)</mo></mtd></mtr></mtable></mrow></math>
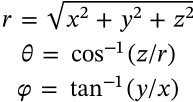
Sperical to Cartesian Coordinates
sperical to cartesian coordinates
$$ \begin{matrix} x = r\, \sin{\theta} \; \cos{\varphi} \\ y = r\, \sin{\theta} \; \sin{\varphi} \\ z = r\, \cos{\theta} \end{matrix} $$
\begin{matrix}
x = r\, \sin{\theta} \; \cos{\varphi} \\
y = r\, \sin{\theta} \; \sin{\varphi} \\
z = r\, \cos{\theta}
\end{matrix}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mtable><mtr><mtd><mi>x</mi><mo>=</mo><mi>r</mi><mspace width="0.167em" /><mi>sin</mi><mrow><mi>θ</mi></mrow><mspace width="0.278em" /><mi>cos</mi><mrow><mi>φ</mi></mrow></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mi>r</mi><mspace width="0.167em" /><mi>sin</mi><mrow><mi>θ</mi></mrow><mspace width="0.278em" /><mi>sin</mi><mrow><mi>φ</mi></mrow></mtd></mtr><mtr><mtd><mi>z</mi><mo>=</mo><mi>r</mi><mspace width="0.167em" /><mi>cos</mi><mrow><mi>θ</mi></mrow></mtd></mtr></mtable></mrow></math>
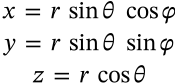
Cylindrical to Spherical Coordinates
cylindrical to spherical coordinates
$$ \begin{matrix} r = \sqrt{\rho^2 + z^2} \\ \theta = \tan^{-1}(\rho/z) \\ \varphi = \varphi \end{matrix} $$
\begin{matrix}
r = \sqrt{\rho^2 + z^2} \\
\theta = \tan^{-1}(\rho/z) \\
\varphi = \varphi
\end{matrix}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mtable><mtr><mtd><mi>r</mi><mo>=</mo><msqrt><mrow><msup><mi>ρ</mi><mn>2</mn></msup><mo>+</mo><msup><mi>z</mi><mn>2</mn></msup></mrow></msqrt></mtd></mtr><mtr><mtd><mi>θ</mi><mo>=</mo><msup><mi>tan</mi><mrow><mo>−</mo><mn>1</mn></mrow></msup><mo stretchy="false">(</mo><mi>ρ</mi><mo>/</mo><mi>z</mi><mo stretchy="false">)</mo></mtd></mtr><mtr><mtd><mi>φ</mi><mo>=</mo><mi>φ</mi></mtd></mtr></mtable></mrow></math>
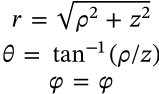
Spherical to Cylindrical Coordinates
spherical to cylindrical coordinates
$$ \begin{matrix} \rho = r\,\sin{\theta} \\ \varphi = \varphi \\ z = r\,\cos{\theta} \end{matrix} $$
\begin{matrix}
\rho = r\,\sin{\theta} \\
\varphi = \varphi \\
z = r\,\cos{\theta}
\end{matrix}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mtable><mtr><mtd><mi>ρ</mi><mo>=</mo><mi>r</mi><mspace width="0.167em" /><mi>sin</mi><mrow><mi>θ</mi></mrow></mtd></mtr><mtr><mtd><mi>φ</mi><mo>=</mo><mi>φ</mi></mtd></mtr><mtr><mtd><mi>z</mi><mo>=</mo><mi>r</mi><mspace width="0.167em" /><mi>cos</mi><mrow><mi>θ</mi></mrow></mtd></mtr></mtable></mrow></math>
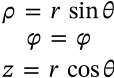
Gradient in Cartesian Coordinates
gradient in cartesian coordinates
$$\nabla f = \frac{\partial f}{\partial x}\boldsymbol{\hat{x}} + \frac{\partial f}{\partial y}\boldsymbol{\hat{y}} + \frac{\partial f}{\partial z}\boldsymbol{\hat{z}}$$
\nabla f = \frac{\partial f}{\partial x}\boldsymbol{\hat{x}} + \frac{\partial f}{\partial y}\boldsymbol{\hat{y}} + \frac{\partial f}{\partial z}\boldsymbol{\hat{z}}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∇</mo><mi>f</mi><mo>=</mo><mfrac><mrow><mo>∂</mo><mi>f</mi></mrow><mrow><mo>∂</mo><mi>x</mi></mrow></mfrac><mrow><mover><mrow><mi mathvariant="bold-italic">x</mi></mrow><mo stretchy="false">^</mo></mover></mrow><mo>+</mo><mfrac><mrow><mo>∂</mo><mi>f</mi></mrow><mrow><mo>∂</mo><mi>y</mi></mrow></mfrac><mrow><mover><mrow><mi mathvariant="bold-italic">y</mi></mrow><mo stretchy="false">^</mo></mover></mrow><mo>+</mo><mfrac><mrow><mo>∂</mo><mi>f</mi></mrow><mrow><mo>∂</mo><mi>z</mi></mrow></mfrac><mrow><mover><mrow><mi mathvariant="bold-italic">z</mi></mrow><mo stretchy="false">^</mo></mover></mrow></mrow></math>
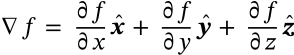
Divergence in Cartesian Coordinates
divergence in cartesian coordinates
$$\nabla \cdot f = \frac{\partial f_x}{\partial x} + \frac{\partial f_y}{\partial y} + \frac{\partial f_z}{\partial z}$$
\nabla \cdot f = \frac{\partial f_x}{\partial x} + \frac{\partial f_y}{\partial y} + \frac{\partial f_z}{\partial z}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∇</mo><mi>·</mi><mi>f</mi><mo>=</mo><mfrac><mrow><mo>∂</mo><msub><mi>f</mi><mi>x</mi></msub></mrow><mrow><mo>∂</mo><mi>x</mi></mrow></mfrac><mo>+</mo><mfrac><mrow><mo>∂</mo><msub><mi>f</mi><mi>y</mi></msub></mrow><mrow><mo>∂</mo><mi>y</mi></mrow></mfrac><mo>+</mo><mfrac><mrow><mo>∂</mo><msub><mi>f</mi><mi>z</mi></msub></mrow><mrow><mo>∂</mo><mi>z</mi></mrow></mfrac></mrow></math>
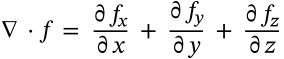
Curl in Cartesian Coordinates
curl in cartesian coordinates
$$\nabla \times f = \left(\frac{\partial f_z}{\partial y} - \frac{\partial f_y}{\partial z}\right)\boldsymbol{\hat{x}} + \left(\frac{\partial f_x}{\partial z} - \frac{\partial f_z}{\partial z}\right)\boldsymbol{\hat{y}} + \left(\frac{\partial f_y}{\partial x} - \frac{\partial f_x}{\partial y}\right)\boldsymbol{\hat{z}}$$
\nabla \times f = \left(\frac{\partial f_z}{\partial y} - \frac{\partial f_y}{\partial z}\right)\boldsymbol{\hat{x}} + \left(\frac{\partial f_x}{\partial z} - \frac{\partial f_z}{\partial z}\right)\boldsymbol{\hat{y}} + \left(\frac{\partial f_y}{\partial x} - \frac{\partial f_x}{\partial y}\right)\boldsymbol{\hat{z}}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∇</mo><mi>×</mi><mi>f</mi><mo>=</mo><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mo>∂</mo><msub><mi>f</mi><mi>z</mi></msub></mrow><mrow><mo>∂</mo><mi>y</mi></mrow></mfrac><mo>−</mo><mfrac><mrow><mo>∂</mo><msub><mi>f</mi><mi>y</mi></msub></mrow><mrow><mo>∂</mo><mi>z</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mrow><mover><mrow><mi mathvariant="bold-italic">x</mi></mrow><mo stretchy="false">^</mo></mover></mrow><mo>+</mo><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mo>∂</mo><msub><mi>f</mi><mi>x</mi></msub></mrow><mrow><mo>∂</mo><mi>z</mi></mrow></mfrac><mo>−</mo><mfrac><mrow><mo>∂</mo><msub><mi>f</mi><mi>z</mi></msub></mrow><mrow><mo>∂</mo><mi>z</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mrow><mover><mrow><mi mathvariant="bold-italic">y</mi></mrow><mo stretchy="false">^</mo></mover></mrow><mo>+</mo><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mo>∂</mo><msub><mi>f</mi><mi>y</mi></msub></mrow><mrow><mo>∂</mo><mi>x</mi></mrow></mfrac><mo>−</mo><mfrac><mrow><mo>∂</mo><msub><mi>f</mi><mi>x</mi></msub></mrow><mrow><mo>∂</mo><mi>y</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mrow><mover><mrow><mi mathvariant="bold-italic">z</mi></mrow><mo stretchy="false">^</mo></mover></mrow></mrow></math>
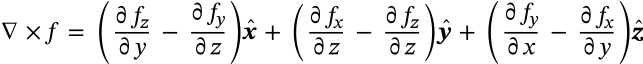
Laplacian in Cartesian Coordinates
laplacian in cartesian coordinates
$$\nabla^2 f = \frac{\partial^2 f}{\partial x^2}\boldsymbol{\hat{x}} + \frac{\partial^2 f}{\partial y^2}\boldsymbol{\hat{y}} + \frac{\partial^2 f}{\partial z^2}\boldsymbol{\hat{z}}$$
\nabla^2 f = \frac{\partial^2 f}{\partial x^2}\boldsymbol{\hat{x}} + \frac{\partial^2 f}{\partial y^2}\boldsymbol{\hat{y}} + \frac{\partial^2 f}{\partial z^2}\boldsymbol{\hat{z}}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msup><mo>∇</mo><mn>2</mn></msup><mi>f</mi><mo>=</mo><mfrac><mrow><msup><mo>∂</mo><mn>2</mn></msup><mi>f</mi></mrow><mrow><mo>∂</mo><msup><mi>x</mi><mn>2</mn></msup></mrow></mfrac><mrow><mover><mrow><mi mathvariant="bold-italic">x</mi></mrow><mo stretchy="false">^</mo></mover></mrow><mo>+</mo><mfrac><mrow><msup><mo>∂</mo><mn>2</mn></msup><mi>f</mi></mrow><mrow><mo>∂</mo><msup><mi>y</mi><mn>2</mn></msup></mrow></mfrac><mrow><mover><mrow><mi mathvariant="bold-italic">y</mi></mrow><mo stretchy="false">^</mo></mover></mrow><mo>+</mo><mfrac><mrow><msup><mo>∂</mo><mn>2</mn></msup><mi>f</mi></mrow><mrow><mo>∂</mo><msup><mi>z</mi><mn>2</mn></msup></mrow></mfrac><mrow><mover><mrow><mi mathvariant="bold-italic">z</mi></mrow><mo stretchy="false">^</mo></mover></mrow></mrow></math>
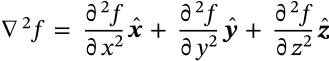
Gradient in Cylindrical Coordinates
gradient in cylindrical coordinates
$$\nabla f = \frac{\partial f}{\partial \rho} \boldsymbol{\hat{\rho}} + \frac{1}{\rho} \frac{\partial f}{\partial \varphi} \boldsymbol{\hat{\varphi}} + \frac{\partial f}{\partial z} \boldsymbol{\hat{z}}$$
\nabla f = \frac{\partial f}{\partial \rho} \boldsymbol{\hat{\rho}} + \frac{1}{\rho} \frac{\partial f}{\partial \varphi} \boldsymbol{\hat{\varphi}} + \frac{\partial f}{\partial z} \boldsymbol{\hat{z}}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∇</mo><mi>f</mi><mo>=</mo><mfrac><mrow><mo>∂</mo><mi>f</mi></mrow><mrow><mo>∂</mo><mi>ρ</mi></mrow></mfrac><mrow><mover><mrow><mi mathvariant="bold-italic">ρ</mi></mrow><mo stretchy="false">^</mo></mover></mrow><mo>+</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>ρ</mi></mrow></mfrac><mfrac><mrow><mo>∂</mo><mi>f</mi></mrow><mrow><mo>∂</mo><mi>φ</mi></mrow></mfrac><mrow><mover><mrow><mi mathvariant="bold-italic">φ</mi></mrow><mo stretchy="false">^</mo></mover></mrow><mo>+</mo><mfrac><mrow><mo>∂</mo><mi>f</mi></mrow><mrow><mo>∂</mo><mi>z</mi></mrow></mfrac><mrow><mover><mrow><mi mathvariant="bold-italic">z</mi></mrow><mo stretchy="false">^</mo></mover></mrow></mrow></math>
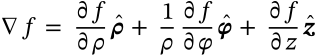
Divergence in Cylindrical Coordinates
divergence in cylindrical coordinates
$$\nabla \cdot \boldsymbol{A} = \frac{1}{\rho}\frac{\partial}{\partial\rho}(\rho A_\rho) + \frac{1}{\rho}\frac{\partial A_\varphi}{\partial \varphi} + \frac{\partial A_z}{\partial z}$$
\nabla \cdot \boldsymbol{A} = \frac{1}{\rho}\frac{\partial}{\partial\rho}(\rho A_\rho) + \frac{1}{\rho}\frac{\partial A_\varphi}{\partial \varphi} + \frac{\partial A_z}{\partial z}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∇</mo><mi>·</mi><mrow><mi mathvariant="bold-italic">A</mi></mrow><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>ρ</mi></mrow></mfrac><mfrac><mrow><mo>∂</mo></mrow><mrow><mo>∂</mo><mi>ρ</mi></mrow></mfrac><mo stretchy="false">(</mo><mi>ρ</mi><msub><mi>A</mi><mi>ρ</mi></msub><mo stretchy="false">)</mo><mo>+</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>ρ</mi></mrow></mfrac><mfrac><mrow><mo>∂</mo><msub><mi>A</mi><mi>φ</mi></msub></mrow><mrow><mo>∂</mo><mi>φ</mi></mrow></mfrac><mo>+</mo><mfrac><mrow><mo>∂</mo><msub><mi>A</mi><mi>z</mi></msub></mrow><mrow><mo>∂</mo><mi>z</mi></mrow></mfrac></mrow></math>
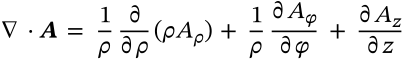
Curl in Cylindrical Coordinates
curl in cylindrical coordinates
$$\nabla \times \boldsymbol{A} = \left(\frac{1}{\rho}\frac{\partial A_z}{\partial \varphi} - \frac{\partial A_\varphi}{\partial z}\right)\boldsymbol{\hat{\rho}} + \\ \left(\frac{\partial A_\rho}{\partial z} - \frac{\partial A_z}{\partial\rho}\right)\boldsymbol{\hat{\varphi}} \\ + \frac{1}{\rho}\left(\frac{\partial}{\partial\rho}(\rho A_\varphi) - \frac{\partial A_\rho}{\partial\varphi}\right)\boldsymbol{\hat{z}}$$
\nabla \times \boldsymbol{A} = \left(\frac{1}{\rho}\frac{\partial A_z}{\partial \varphi} - \frac{\partial A_\varphi}{\partial z}\right)\boldsymbol{\hat{\rho}} + \\ \left(\frac{\partial A_\rho}{\partial z} - \frac{\partial A_z}{\partial\rho}\right)\boldsymbol{\hat{\varphi}} \\ + \frac{1}{\rho}\left(\frac{\partial}{\partial\rho}(\rho A_\varphi) - \frac{\partial A_\rho}{\partial\varphi}\right)\boldsymbol{\hat{z}}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∇</mo><mi>×</mi><mrow><mi mathvariant="bold-italic">A</mi></mrow><mo>=</mo><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>ρ</mi></mrow></mfrac><mfrac><mrow><mo>∂</mo><msub><mi>A</mi><mi>z</mi></msub></mrow><mrow><mo>∂</mo><mi>φ</mi></mrow></mfrac><mo>−</mo><mfrac><mrow><mo>∂</mo><msub><mi>A</mi><mi>φ</mi></msub></mrow><mrow><mo>∂</mo><mi>z</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mrow><mover><mrow><mi mathvariant="bold-italic">ρ</mi></mrow><mo stretchy="false">^</mo></mover></mrow><mo>+</mo><mspace linebreak="newline" /><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mo>∂</mo><msub><mi>A</mi><mi>ρ</mi></msub></mrow><mrow><mo>∂</mo><mi>z</mi></mrow></mfrac><mo>−</mo><mfrac><mrow><mo>∂</mo><msub><mi>A</mi><mi>z</mi></msub></mrow><mrow><mo>∂</mo><mi>ρ</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mrow><mover><mrow><mi mathvariant="bold-italic">φ</mi></mrow><mo stretchy="false">^</mo></mover></mrow><mspace linebreak="newline" /><mo>+</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>ρ</mi></mrow></mfrac><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mo>∂</mo></mrow><mrow><mo>∂</mo><mi>ρ</mi></mrow></mfrac><mo stretchy="false">(</mo><mi>ρ</mi><msub><mi>A</mi><mi>φ</mi></msub><mo stretchy="false">)</mo><mo>−</mo><mfrac><mrow><mo>∂</mo><msub><mi>A</mi><mi>ρ</mi></msub></mrow><mrow><mo>∂</mo><mi>φ</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mrow><mover><mrow><mi mathvariant="bold-italic">z</mi></mrow><mo stretchy="false">^</mo></mover></mrow></mrow></math>
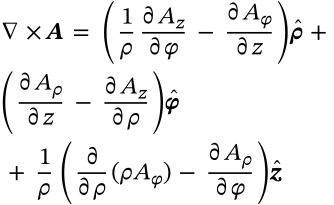
Laplacian in Cylindrical Coordinates
laplacian in cylindrical coordinates
$$\nabla^2 f = \frac{1}{\rho}\frac{\partial}{\partial\rho}\left(\rho\frac{\partial f}{\partial \rho}\right) + \frac{1}{\rho^2}\frac{\partial^2 f}{\partial \varphi^2} + \frac{\partial^2 f}{\partial z^2}$$
\nabla^2 f = \frac{1}{\rho}\frac{\partial}{\partial\rho}\left(\rho\frac{\partial f}{\partial \rho}\right) + \frac{1}{\rho^2}\frac{\partial^2 f}{\partial \varphi^2} + \frac{\partial^2 f}{\partial z^2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msup><mo>∇</mo><mn>2</mn></msup><mi>f</mi><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>ρ</mi></mrow></mfrac><mfrac><mrow><mo>∂</mo></mrow><mrow><mo>∂</mo><mi>ρ</mi></mrow></mfrac><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mi>ρ</mi><mfrac><mrow><mo>∂</mo><mi>f</mi></mrow><mrow><mo>∂</mo><mi>ρ</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mo>+</mo><mfrac><mrow><mn>1</mn></mrow><mrow><msup><mi>ρ</mi><mn>2</mn></msup></mrow></mfrac><mfrac><mrow><msup><mo>∂</mo><mn>2</mn></msup><mi>f</mi></mrow><mrow><mo>∂</mo><msup><mi>φ</mi><mn>2</mn></msup></mrow></mfrac><mo>+</mo><mfrac><mrow><msup><mo>∂</mo><mn>2</mn></msup><mi>f</mi></mrow><mrow><mo>∂</mo><msup><mi>z</mi><mn>2</mn></msup></mrow></mfrac></mrow></math>
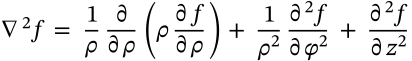
Gradient in Spherical Coordinates
gradient in spherical coordinates
$$\nabla f = \frac{\partial f}{\partial r} \boldsymbol{\hat{r}} + \frac{1}{r} \frac{\partial f}{\partial \theta} \boldsymbol{\hat{\theta}} + \frac{1}{r\,\sin{\theta}}\frac{\partial f}{\partial \varphi} \boldsymbol{\hat{\varphi}}$$
\nabla f = \frac{\partial f}{\partial r} \boldsymbol{\hat{r}} + \frac{1}{r} \frac{\partial f}{\partial \theta} \boldsymbol{\hat{\theta}} + \frac{1}{r\,\sin{\theta}}\frac{\partial f}{\partial \varphi} \boldsymbol{\hat{\varphi}}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∇</mo><mi>f</mi><mo>=</mo><mfrac><mrow><mo>∂</mo><mi>f</mi></mrow><mrow><mo>∂</mo><mi>r</mi></mrow></mfrac><mrow><mover><mrow><mi mathvariant="bold-italic">r</mi></mrow><mo stretchy="false">^</mo></mover></mrow><mo>+</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>r</mi></mrow></mfrac><mfrac><mrow><mo>∂</mo><mi>f</mi></mrow><mrow><mo>∂</mo><mi>θ</mi></mrow></mfrac><mrow><mover><mrow><mi mathvariant="bold-italic">θ</mi></mrow><mo stretchy="false">^</mo></mover></mrow><mo>+</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>r</mi><mspace width="0.167em" /><mi>sin</mi><mrow><mi>θ</mi></mrow></mrow></mfrac><mfrac><mrow><mo>∂</mo><mi>f</mi></mrow><mrow><mo>∂</mo><mi>φ</mi></mrow></mfrac><mrow><mover><mrow><mi mathvariant="bold-italic">φ</mi></mrow><mo stretchy="false">^</mo></mover></mrow></mrow></math>
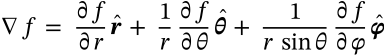
Divergence in Spherical Coordinates
divergence in spherical coordinates
$$\nabla \cdot \boldsymbol{A} = \frac{1}{r^2}\frac{\partial}{\partial r}(r^2 A_r) + \frac{1}{r\,\sin{\theta}}\frac{\partial}{\partial \theta}(\sin{\theta A_\theta}) + \frac{1}{r\,\sin{\theta}}\frac{\partial A_\varphi}{\partial \varphi}$$
\nabla \cdot \boldsymbol{A} = \frac{1}{r^2}\frac{\partial}{\partial r}(r^2 A_r) + \frac{1}{r\,\sin{\theta}}\frac{\partial}{\partial \theta}(\sin{\theta A_\theta}) + \frac{1}{r\,\sin{\theta}}\frac{\partial A_\varphi}{\partial \varphi}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∇</mo><mi>·</mi><mrow><mi mathvariant="bold-italic">A</mi></mrow><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><msup><mi>r</mi><mn>2</mn></msup></mrow></mfrac><mfrac><mrow><mo>∂</mo></mrow><mrow><mo>∂</mo><mi>r</mi></mrow></mfrac><mo stretchy="false">(</mo><msup><mi>r</mi><mn>2</mn></msup><msub><mi>A</mi><mi>r</mi></msub><mo stretchy="false">)</mo><mo>+</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>r</mi><mspace width="0.167em" /><mi>sin</mi><mrow><mi>θ</mi></mrow></mrow></mfrac><mfrac><mrow><mo>∂</mo></mrow><mrow><mo>∂</mo><mi>θ</mi></mrow></mfrac><mo stretchy="false">(</mo><mi>sin</mi><mrow><mi>θ</mi><msub><mi>A</mi><mi>θ</mi></msub></mrow><mo stretchy="false">)</mo><mo>+</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>r</mi><mspace width="0.167em" /><mi>sin</mi><mrow><mi>θ</mi></mrow></mrow></mfrac><mfrac><mrow><mo>∂</mo><msub><mi>A</mi><mi>φ</mi></msub></mrow><mrow><mo>∂</mo><mi>φ</mi></mrow></mfrac></mrow></math>
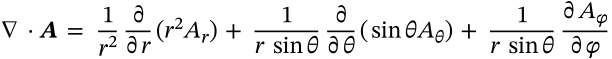
Curl in Spherical Coordinates
curl in spherical coordinates
$$\nabla \times \boldsymbol{A} = \frac{1}{r\,\sin{\theta}} \left(\frac{\partial}{\partial \theta}(A_\varphi \sin{\theta}) - \frac{\partial A_\theta}{\partial\varphi}\right)\boldsymbol{\hat{r}} \\ + \frac{1}{r}\left(\frac{1}{\sin{\theta}}\frac{\partial A_r}{\partial\varphi} - \frac{\partial}{\partial r}(rA_\varphi)\right)\boldsymbol{\hat{\theta}} \\ + \frac{1}{r}\left(\frac{\partial}{\partial r}(rA_\theta) - \frac{\partial A_r}{\partial\theta}\right)\boldsymbol{\hat{\varphi}} $$
\nabla \times \boldsymbol{A} =
\frac{1}{r\,\sin{\theta}} \left(\frac{\partial}{\partial \theta}(A_\varphi \sin{\theta}) - \frac{\partial A_\theta}{\partial\varphi}\right)\boldsymbol{\hat{r}} \\
+ \frac{1}{r}\left(\frac{1}{\sin{\theta}}\frac{\partial A_r}{\partial\varphi} - \frac{\partial}{\partial r}(rA_\varphi)\right)\boldsymbol{\hat{\theta}} \\
+ \frac{1}{r}\left(\frac{\partial}{\partial r}(rA_\theta) - \frac{\partial A_r}{\partial\theta}\right)\boldsymbol{\hat{\varphi}}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∇</mo><mi>×</mi><mrow><mi mathvariant="bold-italic">A</mi></mrow><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>r</mi><mspace width="0.167em" /><mi>sin</mi><mrow><mi>θ</mi></mrow></mrow></mfrac><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mo>∂</mo></mrow><mrow><mo>∂</mo><mi>θ</mi></mrow></mfrac><mo stretchy="false">(</mo><msub><mi>A</mi><mi>φ</mi></msub><mi>sin</mi><mrow><mi>θ</mi></mrow><mo stretchy="false">)</mo><mo>−</mo><mfrac><mrow><mo>∂</mo><msub><mi>A</mi><mi>θ</mi></msub></mrow><mrow><mo>∂</mo><mi>φ</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mrow><mover><mrow><mi mathvariant="bold-italic">r</mi></mrow><mo stretchy="false">^</mo></mover></mrow><mspace linebreak="newline" /><mo>+</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>r</mi></mrow></mfrac><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>sin</mi><mrow><mi>θ</mi></mrow></mrow></mfrac><mfrac><mrow><mo>∂</mo><msub><mi>A</mi><mi>r</mi></msub></mrow><mrow><mo>∂</mo><mi>φ</mi></mrow></mfrac><mo>−</mo><mfrac><mrow><mo>∂</mo></mrow><mrow><mo>∂</mo><mi>r</mi></mrow></mfrac><mo stretchy="false">(</mo><mi>r</mi><msub><mi>A</mi><mi>φ</mi></msub><mo stretchy="false">)</mo><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mrow><mover><mrow><mi mathvariant="bold-italic">θ</mi></mrow><mo stretchy="false">^</mo></mover></mrow><mspace linebreak="newline" /><mo>+</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>r</mi></mrow></mfrac><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mo>∂</mo></mrow><mrow><mo>∂</mo><mi>r</mi></mrow></mfrac><mo stretchy="false">(</mo><mi>r</mi><msub><mi>A</mi><mi>θ</mi></msub><mo stretchy="false">)</mo><mo>−</mo><mfrac><mrow><mo>∂</mo><msub><mi>A</mi><mi>r</mi></msub></mrow><mrow><mo>∂</mo><mi>θ</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mrow><mover><mrow><mi mathvariant="bold-italic">φ</mi></mrow><mo stretchy="false">^</mo></mover></mrow></mrow></math>
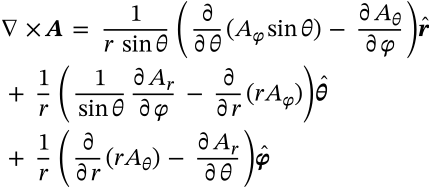
Laplacian in Spherical Coordinates
laplacian in spherical coordinates
$$\nabla^2 f = \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial f}{\partial r}\right) + \frac{1}{r^2 \sin{\theta}}\frac{\partial}{\partial \theta}\left(\sin{\theta} \frac{\partial f}{\partial\theta}\right) + \frac{1}{r^2 \sin{\theta}}\frac{\partial^2 f}{\partial \varphi^2}$$
\nabla^2 f = \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial f}{\partial r}\right) + \frac{1}{r^2 \sin{\theta}}\frac{\partial}{\partial \theta}\left(\sin{\theta} \frac{\partial f}{\partial\theta}\right) + \frac{1}{r^2 \sin{\theta}}\frac{\partial^2 f}{\partial \varphi^2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msup><mo>∇</mo><mn>2</mn></msup><mi>f</mi><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><msup><mi>r</mi><mn>2</mn></msup></mrow></mfrac><mfrac><mrow><mo>∂</mo></mrow><mrow><mo>∂</mo><mi>r</mi></mrow></mfrac><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><msup><mi>r</mi><mn>2</mn></msup><mfrac><mrow><mo>∂</mo><mi>f</mi></mrow><mrow><mo>∂</mo><mi>r</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mo>+</mo><mfrac><mrow><mn>1</mn></mrow><mrow><msup><mi>r</mi><mn>2</mn></msup><mi>sin</mi><mrow><mi>θ</mi></mrow></mrow></mfrac><mfrac><mrow><mo>∂</mo></mrow><mrow><mo>∂</mo><mi>θ</mi></mrow></mfrac><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mi>sin</mi><mrow><mi>θ</mi></mrow><mfrac><mrow><mo>∂</mo><mi>f</mi></mrow><mrow><mo>∂</mo><mi>θ</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mo>+</mo><mfrac><mrow><mn>1</mn></mrow><mrow><msup><mi>r</mi><mn>2</mn></msup><mi>sin</mi><mrow><mi>θ</mi></mrow></mrow></mfrac><mfrac><mrow><msup><mo>∂</mo><mn>2</mn></msup><mi>f</mi></mrow><mrow><mo>∂</mo><msup><mi>φ</mi><mn>2</mn></msup></mrow></mfrac></mrow></math>
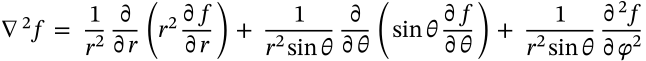
Derivative
derivative calculus
$$\frac{d}{dx} f(x) = \lim_{\Delta \to 0} \frac{f(x+\Delta) - f(x)}{\Delta}$$
\frac{d}{dx} f(x) = \lim_{\Delta \to 0} \frac{f(x+\Delta) - f(x)}{\Delta}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mfrac><mrow><mi>d</mi></mrow><mrow><mi>d</mi><mi>x</mi></mrow></mfrac><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><msub><mo>lim</mo><mrow><mi>Δ</mi><mo>→</mo><mn>0</mn></mrow></msub><mfrac><mrow><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo>+</mo><mi>Δ</mi><mo stretchy="false">)</mo><mo>−</mo><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo></mrow><mrow><mi>Δ</mi></mrow></mfrac></mrow></math>
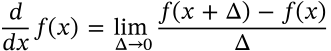
Fundamental Theorem of Calculus
fundamental theorem of calculus
$$\frac{d}{dx} \int_a^x f(t) dt = f(x)$$
\frac{d}{dx} \int_a^x f(t) dt = f(x)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mfrac><mrow><mi>d</mi></mrow><mrow><mi>d</mi><mi>x</mi></mrow></mfrac><msubsup><mo>∫</mo><mi>a</mi><mi>x</mi></msubsup><mi>f</mi><mo stretchy="false">(</mo><mi>t</mi><mo stretchy="false">)</mo><mi>d</mi><mi>t</mi><mo>=</mo><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo></mrow></math>
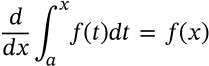
L'Hopital's Rule
l'hopital's rule calculus
$$\lim_{x \to c} \frac{f(x)}{g(x)} = \lim_{x \to c} \frac{f'(x)}{g'(x)}$$
\lim_{x \to c} \frac{f(x)}{g(x)} = \lim_{x \to c} \frac{f'(x)}{g'(x)}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msub><mo>lim</mo><mrow><mi>x</mi><mo>→</mo><mi>c</mi></mrow></msub><mfrac><mrow><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo></mrow><mrow><mi>g</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo></mrow></mfrac><mo>=</mo><msub><mo>lim</mo><mrow><mi>x</mi><mo>→</mo><mi>c</mi></mrow></msub><mfrac><mrow><msup><mi>f</mi><mi>′</mi></msup><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo></mrow><mrow><msup><mi>g</mi><mi>′</mi></msup><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo></mrow></mfrac></mrow></math>
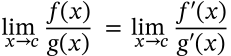
Derivative Chain Rule
derivative chain rule calculus
$$\frac{d}{dx} [f(g(x))] = f' (g(x)) g' (x)$$
\frac{d}{dx} [f(g(x))] = f' (g(x)) g' (x)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mfrac><mrow><mi>d</mi></mrow><mrow><mi>d</mi><mi>x</mi></mrow></mfrac><mo stretchy="false">[</mo><mi>f</mi><mo stretchy="false">(</mo><mi>g</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo stretchy="false">)</mo><mo stretchy="false">]</mo><mo>=</mo><msup><mi>f</mi><mi>′</mi></msup><mo stretchy="false">(</mo><mi>g</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo stretchy="false">)</mo><msup><mi>g</mi><mi>′</mi></msup><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo></mrow></math>
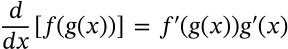
Derivative Product Rule
derivative product rule calculus
$$\frac{d}{dx} [f(x)g(x)] = f(x) g'(x) + f'(x)g(x)$$
\frac{d}{dx} [f(x)g(x)] = f(x) g'(x) + f'(x)g(x)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mfrac><mrow><mi>d</mi></mrow><mrow><mi>d</mi><mi>x</mi></mrow></mfrac><mo stretchy="false">[</mo><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mi>g</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo stretchy="false">]</mo><mo>=</mo><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><msup><mi>g</mi><mi>′</mi></msup><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>+</mo><msup><mi>f</mi><mi>′</mi></msup><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mi>g</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo></mrow></math>
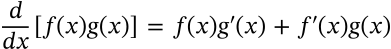
Derivative Quotient Rule
derivative quotient rule calculus
$$\left(\frac{f(x)}{g(x)}\right)' = \frac{g(x)f'(x) - f(x)g'(x)}{g(x)^2}$$
\left(\frac{f(x)}{g(x)}\right)' = \frac{g(x)f'(x) - f(x)g'(x)}{g(x)^2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msup><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo></mrow><mrow><mi>g</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mi>′</mi></msup><mo>=</mo><mfrac><mrow><mi>g</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><msup><mi>f</mi><mi>′</mi></msup><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>−</mo><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><msup><mi>g</mi><mi>′</mi></msup><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo></mrow><mrow><mi>g</mi><mo stretchy="false">(</mo><mi>x</mi><msup><mo stretchy="false">)</mo><mn>2</mn></msup></mrow></mfrac></mrow></math>
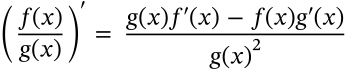
Integration by Parts
integration by parts calculus
$$\int u dv = uv - \int v du$$
\int u dv = uv - \int v du
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∫</mo><mi>u</mi><mi>d</mi><mi>v</mi><mo>=</mo><mi>u</mi><mi>v</mi><mo>−</mo><mo>∫</mo><mi>v</mi><mi>d</mi><mi>u</mi></mrow></math>
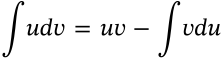
Derivative of Constant
derivative of constant calculus
$$\frac{d}{dx}C = 0$$
\frac{d}{dx}C = 0
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mfrac><mrow><mi>d</mi></mrow><mrow><mi>d</mi><mi>x</mi></mrow></mfrac><mi>C</mi><mo>=</mo><mn>0</mn></mrow></math>
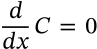
Derivative of Power
derivative of power calculus
$$\frac{d}{dx}x^n = nx^{n-1}$$
\frac{d}{dx}x^n = nx^{n-1}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mfrac><mrow><mi>d</mi></mrow><mrow><mi>d</mi><mi>x</mi></mrow></mfrac><msup><mi>x</mi><mi>n</mi></msup><mo>=</mo><mi>n</mi><msup><mi>x</mi><mrow><mi>n</mi><mo>−</mo><mn>1</mn></mrow></msup></mrow></math>
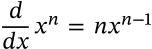
Derivative of Exponential
derivative of exponential calculus
$$\frac{d}{dx}e^{nx} = ke^{nx}$$
\frac{d}{dx}e^{nx} = ke^{nx}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mfrac><mrow><mi>d</mi></mrow><mrow><mi>d</mi><mi>x</mi></mrow></mfrac><msup><mi>e</mi><mrow><mi>n</mi><mi>x</mi></mrow></msup><mo>=</mo><mi>k</mi><msup><mi>e</mi><mrow><mi>n</mi><mi>x</mi></mrow></msup></mrow></math>
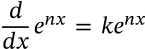
Derivative of Logarithm
derivative of logarithm calculus
$$\frac{d}{dx} \ln{x} = \frac{1}{x}$$
\frac{d}{dx} \ln{x} = \frac{1}{x}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mfrac><mrow><mi>d</mi></mrow><mrow><mi>d</mi><mi>x</mi></mrow></mfrac><mi>ln</mi><mrow><mi>x</mi></mrow><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>x</mi></mrow></mfrac></mrow></math>
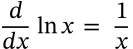
Derivative of Sine
derivative of sine calculus
$$\frac{d}{dx}\sin x = \cos x$$
\frac{d}{dx}\sin x = \cos x
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mfrac><mrow><mi>d</mi></mrow><mrow><mi>d</mi><mi>x</mi></mrow></mfrac><mi>sin</mi><mi>x</mi><mo>=</mo><mi>cos</mi><mi>x</mi></mrow></math>
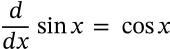
Derivative of Cosine
derivative of cosine calculus
$$\frac{d}{dx}\cos x = -\sin x$$
\frac{d}{dx}\cos x = -\sin x
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mfrac><mrow><mi>d</mi></mrow><mrow><mi>d</mi><mi>x</mi></mrow></mfrac><mi>cos</mi><mi>x</mi><mo>=</mo><mo>−</mo><mi>sin</mi><mi>x</mi></mrow></math>
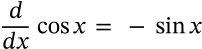
Derivative of Tangent
derivative of tangent calculus
$$\frac{d}{dx}\tan x = \sec^2 x$$
\frac{d}{dx}\tan x = \sec^2 x
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mfrac><mrow><mi>d</mi></mrow><mrow><mi>d</mi><mi>x</mi></mrow></mfrac><mi>tan</mi><mi>x</mi><mo>=</mo><msup><mi>sec</mi><mn>2</mn></msup><mi>x</mi></mrow></math>
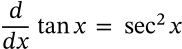
Integral of Sine
integral of sine calculus
$$\int \sin(nx) dx = -\frac{1}{n}\cos(nx) + c$$
\int \sin(nx) dx = -\frac{1}{n}\cos(nx) + c
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∫</mo><mi>sin</mi><mo stretchy="false">(</mo><mi>n</mi><mi>x</mi><mo stretchy="false">)</mo><mi>d</mi><mi>x</mi><mo>=</mo><mo>−</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>n</mi></mrow></mfrac><mi>cos</mi><mo stretchy="false">(</mo><mi>n</mi><mi>x</mi><mo stretchy="false">)</mo><mo>+</mo><mi>c</mi></mrow></math>
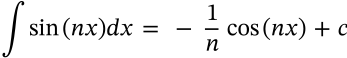
Integral of Cosine
integral of cosine calculus
$$\int \cos(nx) dx = \frac{1}{n}\sin(nx) + c$$
\int \cos(nx) dx = \frac{1}{n}\sin(nx) + c
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∫</mo><mi>cos</mi><mo stretchy="false">(</mo><mi>n</mi><mi>x</mi><mo stretchy="false">)</mo><mi>d</mi><mi>x</mi><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>n</mi></mrow></mfrac><mi>sin</mi><mo stretchy="false">(</mo><mi>n</mi><mi>x</mi><mo stretchy="false">)</mo><mo>+</mo><mi>c</mi></mrow></math>
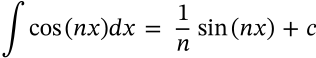
Integral of Tangent
integral of tangent calculus
$$\int \tan(nx) dx = -\frac{1}{n}\ln|\cos(nx)| + c$$
\int \tan(nx) dx = -\frac{1}{n}\ln|\cos(nx)| + c
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∫</mo><mi>tan</mi><mo stretchy="false">(</mo><mi>n</mi><mi>x</mi><mo stretchy="false">)</mo><mi>d</mi><mi>x</mi><mo>=</mo><mo>−</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>n</mi></mrow></mfrac><mi>ln</mi><mo stretchy="false">|</mo><mi>cos</mi><mo stretchy="false">(</mo><mi>n</mi><mi>x</mi><mo stretchy="false">)</mo><mo stretchy="false">|</mo><mo>+</mo><mi>c</mi></mrow></math>
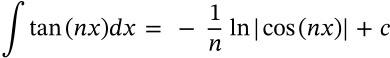
Integral of Power
integral of power calculus
$$\int x^n dx = \frac{1}{n+1} x^{n+1} + c$$
\int x^n dx = \frac{1}{n+1} x^{n+1} + c
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∫</mo><msup><mi>x</mi><mi>n</mi></msup><mi>d</mi><mi>x</mi><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>n</mi><mo>+</mo><mn>1</mn></mrow></mfrac><msup><mi>x</mi><mrow><mi>n</mi><mo>+</mo><mn>1</mn></mrow></msup><mo>+</mo><mi>c</mi></mrow></math>
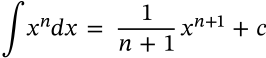
Integral of Power
integral of power calculus
$$\int n^x dx = \frac{1}{\ln{n}} n^x + c$$
\int n^x dx = \frac{1}{\ln{n}} n^x + c
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∫</mo><msup><mi>n</mi><mi>x</mi></msup><mi>d</mi><mi>x</mi><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>ln</mi><mrow><mi>n</mi></mrow></mrow></mfrac><msup><mi>n</mi><mi>x</mi></msup><mo>+</mo><mi>c</mi></mrow></math>
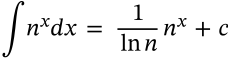
Integral of Reciprocal
integral of reciprocal calculus
$$\int \frac{1}{x} dx = \ln |x| + c$$
\int \frac{1}{x} dx = \ln |x| + c
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∫</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>x</mi></mrow></mfrac><mi>d</mi><mi>x</mi><mo>=</mo><mi>ln</mi><mo stretchy="false">|</mo><mi>x</mi><mo stretchy="false">|</mo><mo>+</mo><mi>c</mi></mrow></math>
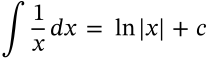
Integral of Exponential
integral of exponential calculus
$$\int e^{nx} dx = \frac{1}{n} e^{nx} + c$$
\int e^{nx} dx = \frac{1}{n} e^{nx} + c
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∫</mo><msup><mi>e</mi><mrow><mi>n</mi><mi>x</mi></mrow></msup><mi>d</mi><mi>x</mi><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>n</mi></mrow></mfrac><msup><mi>e</mi><mrow><mi>n</mi><mi>x</mi></mrow></msup><mo>+</mo><mi>c</mi></mrow></math>
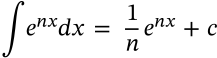
Integral of Logarithm
integral of logarithm calculus
$$\int \ln{x} dx = x \ln{x} - x + C$$
\int \ln{x} dx = x \ln{x} - x + C
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo>∫</mo><mi>ln</mi><mrow><mi>x</mi></mrow><mi>d</mi><mi>x</mi><mo>=</mo><mi>x</mi><mi>ln</mi><mrow><mi>x</mi></mrow><mo>−</mo><mi>x</mi><mo>+</mo><mi>C</mi></mrow></math>
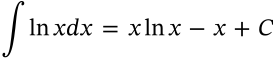
Taylor Series
taylor series
$$f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n$$
f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><msubsup><mo>∑</mo><mrow><mi>n</mi><mo>=</mo><mn>0</mn></mrow><mrow><mo>∞</mo></mrow></msubsup><mfrac><mrow><msup><mi>f</mi><mrow><mo stretchy="false">(</mo><mi>n</mi><mo stretchy="false">)</mo></mrow></msup><mo stretchy="false">(</mo><mi>a</mi><mo stretchy="false">)</mo></mrow><mrow><mi>n</mi><mo>!</mo></mrow></mfrac><mo stretchy="false">(</mo><mi>x</mi><mo>−</mo><mi>a</mi><msup><mo stretchy="false">)</mo><mi>n</mi></msup></mrow></math>
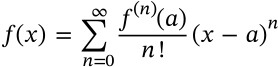
Fourier Series
fourier series
$$f(x) = a_0 + \sum_{n=1}^{\infty} a_n \cos\left(nx\frac{\pi}{L}\right) + \sum_{n=1}^{\infty} b_n \sin\left(nx\frac{\pi}{L}\right)$$
f(x) = a_0 + \sum_{n=1}^{\infty} a_n \cos\left(nx\frac{\pi}{L}\right) + \sum_{n=1}^{\infty} b_n \sin\left(nx\frac{\pi}{L}\right)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><msub><mi>a</mi><mn>0</mn></msub><mo>+</mo><msubsup><mo>∑</mo><mrow><mi>n</mi><mo>=</mo><mn>1</mn></mrow><mrow><mo>∞</mo></mrow></msubsup><msub><mi>a</mi><mi>n</mi></msub><mi>cos</mi><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mi>n</mi><mi>x</mi><mfrac><mrow><mi>π</mi></mrow><mrow><mi>L</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mo>+</mo><msubsup><mo>∑</mo><mrow><mi>n</mi><mo>=</mo><mn>1</mn></mrow><mrow><mo>∞</mo></mrow></msubsup><msub><mi>b</mi><mi>n</mi></msub><mi>sin</mi><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mi>n</mi><mi>x</mi><mfrac><mrow><mi>π</mi></mrow><mrow><mi>L</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow></mrow></math>
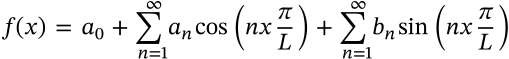
Fourier Transform
fourier transform
$$F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i\omega t} dt$$
F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i\omega t} dt
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>F</mi><mo stretchy="false">(</mo><mi>ω</mi><mo stretchy="false">)</mo><mo>=</mo><msubsup><mo>∫</mo><mrow><mo>−</mo><mo>∞</mo></mrow><mrow><mo>∞</mo></mrow></msubsup><mi>f</mi><mo stretchy="false">(</mo><mi>t</mi><mo stretchy="false">)</mo><msup><mi>e</mi><mrow><mo>−</mo><mi>i</mi><mi>ω</mi><mi>t</mi></mrow></msup><mi>d</mi><mi>t</mi></mrow></math>
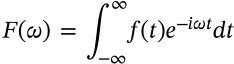
Inverse Fourier Transform
inverse fourier transform
$$f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{i\omega t} d\omega$$
f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{i\omega t} d\omega
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>f</mi><mo stretchy="false">(</mo><mi>t</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn><mi>π</mi></mrow></mfrac><msubsup><mo>∫</mo><mrow><mo>−</mo><mo>∞</mo></mrow><mrow><mo>∞</mo></mrow></msubsup><mi>F</mi><mo stretchy="false">(</mo><mi>ω</mi><mo stretchy="false">)</mo><msup><mi>e</mi><mrow><mi>i</mi><mi>ω</mi><mi>t</mi></mrow></msup><mi>d</mi><mi>ω</mi></mrow></math>
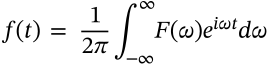
Error Function
error function
$$\mathrm{erf}(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} dt$$
\mathrm{erf}(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} dt
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mrow><mi mathvariant="normal">e</mi><mi mathvariant="normal">r</mi><mi mathvariant="normal">f</mi></mrow><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mn>2</mn></mrow><mrow><msqrt><mrow><mi>π</mi></mrow></msqrt></mrow></mfrac><msubsup><mo>∫</mo><mn>0</mn><mi>x</mi></msubsup><msup><mi>e</mi><mrow><mo>−</mo><msup><mi>t</mi><mn>2</mn></msup></mrow></msup><mi>d</mi><mi>t</mi></mrow></math>
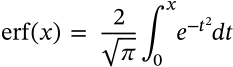
Gamma Function
gamma function
$$\Gamma(z) = \int_0^\infty x^{z-1}e^{-x} dx$$
\Gamma(z) = \int_0^\infty x^{z-1}e^{-x} dx
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>Γ</mi><mo stretchy="false">(</mo><mi>z</mi><mo stretchy="false">)</mo><mo>=</mo><msubsup><mo>∫</mo><mn>0</mn><mo>∞</mo></msubsup><msup><mi>x</mi><mrow><mi>z</mi><mo>−</mo><mn>1</mn></mrow></msup><msup><mi>e</mi><mrow><mo>−</mo><mi>x</mi></mrow></msup><mi>d</mi><mi>x</mi></mrow></math>
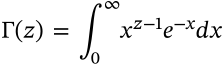
Standard Deviation of a Sample
standard deviation of a sample
$$s = \sqrt{\frac{1}{N-1} \sum_{i=1}^N (x_i - \overline{x})^2}$$
s = \sqrt{\frac{1}{N-1} \sum_{i=1}^N (x_i - \overline{x})^2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>s</mi><mo>=</mo><msqrt><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mi>N</mi><mo>−</mo><mn>1</mn></mrow></mfrac><msubsup><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>N</mi></msubsup><mo stretchy="false">(</mo><msub><mi>x</mi><mi>i</mi></msub><mo>−</mo><mover><mrow><mi>x</mi></mrow><mo accent="true">―</mo></mover><msup><mo stretchy="false">)</mo><mn>2</mn></msup></mrow></msqrt></mrow></math>
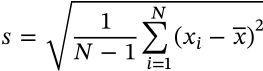
Standard Deviation of a Population
standard deviation of a population
$$\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2}$$
\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>σ</mi><mo>=</mo><msqrt><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mi>N</mi></mrow></mfrac><msubsup><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>N</mi></msubsup><mo stretchy="false">(</mo><msub><mi>x</mi><mi>i</mi></msub><mo>−</mo><mi>μ</mi><msup><mo stretchy="false">)</mo><mn>2</mn></msup></mrow></msqrt></mrow></math>
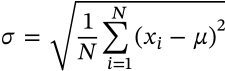
Standard Error of the Mean
standard error of the mean
$$SE = \frac{s}{\sqrt{n}}$$
SE = \frac{s}{\sqrt{n}}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>S</mi><mi>E</mi><mo>=</mo><mfrac><mrow><mi>s</mi></mrow><mrow><msqrt><mrow><mi>n</mi></mrow></msqrt></mrow></mfrac></mrow></math>
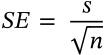
Normal Distribution PDF
normal distribution pdf gaussian
$$f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}$$
f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mi>σ</mi><msqrt><mrow><mn>2</mn><mi>π</mi></mrow></msqrt></mrow></mfrac><msup><mi>e</mi><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><msup><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mi>x</mi><mo>−</mo><mi>μ</mi></mrow><mrow><mi>σ</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mn>2</mn></msup></mrow></msup></mrow></math>
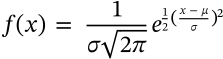
Normal Distribution CDF
normal distribution cdf gaussian
$$\Phi(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^x e^{-t^2/2} dt$$
\Phi(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^x e^{-t^2/2} dt
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>Φ</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><msqrt><mrow><mn>2</mn><mi>π</mi></mrow></msqrt></mrow></mfrac><msubsup><mo>∫</mo><mrow><mo>−</mo><mo>∞</mo></mrow><mi>x</mi></msubsup><msup><mi>e</mi><mrow><mo>−</mo><msup><mi>t</mi><mn>2</mn></msup><mo>/</mo><mn>2</mn></mrow></msup><mi>d</mi><mi>t</mi></mrow></math>
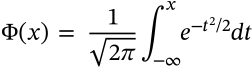
Gamma Distribution PDF
gamma distribution pdf
$$f(x) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha-1}e^{-\beta x}$$
f(x) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha-1}e^{-\beta x}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><msup><mi>β</mi><mi>α</mi></msup></mrow><mrow><mi>Γ</mi><mo stretchy="false">(</mo><mi>α</mi><mo stretchy="false">)</mo></mrow></mfrac><msup><mi>x</mi><mrow><mi>α</mi><mo>−</mo><mn>1</mn></mrow></msup><msup><mi>e</mi><mrow><mo>−</mo><mi>β</mi><mi>x</mi></mrow></msup></mrow></math>
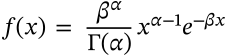
Poisson Distribution PMF
poisson distribution pmf
$$f(x) = \frac{\lambda^k e^{-\lambda}}{k!}$$
f(x) = \frac{\lambda^k e^{-\lambda}}{k!}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><msup><mi>λ</mi><mi>k</mi></msup><msup><mi>e</mi><mrow><mo>−</mo><mi>λ</mi></mrow></msup></mrow><mrow><mi>k</mi><mo>!</mo></mrow></mfrac></mrow></math>
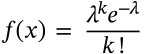
Binomial Coefficient
binomial coefficient
$$\binom{n}{k} = \frac{n!}{k!(n-k)!}$$
\binom{n}{k} = \frac{n!}{k!(n-k)!}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mo minsize="2.047em" maxsize="2.047em">(</mo><mfrac linethickness="0"><mrow><mi>n</mi></mrow><mrow><mi>k</mi></mrow></mfrac><mo minsize="2.047em" maxsize="2.047em">)</mo><mo>=</mo><mfrac><mrow><mi>n</mi><mo>!</mo></mrow><mrow><mi>k</mi><mo>!</mo><mo stretchy="false">(</mo><mi>n</mi><mo>−</mo><mi>k</mi><mo stretchy="false">)</mo><mo>!</mo></mrow></mfrac></mrow></math>
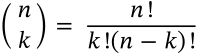
Binomial Distribution PMF
binomial distribution pmf
$$f(x) = \binom{n}{k} p^k q^{n-k}$$
f(x) = \binom{n}{k} p^k q^{n-k}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mo minsize="2.047em" maxsize="2.047em">(</mo><mfrac linethickness="0"><mrow><mi>n</mi></mrow><mrow><mi>k</mi></mrow></mfrac><mo minsize="2.047em" maxsize="2.047em">)</mo><msup><mi>p</mi><mi>k</mi></msup><msup><mi>q</mi><mrow><mi>n</mi><mo>−</mo><mi>k</mi></mrow></msup></mrow></math>
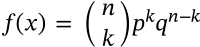
Student's-t Distribution PDF
student's-t distribution pdf
$$f(x) = \frac{1}{\sqrt{\nu \pi}} \frac{\Gamma\left(\frac{\nu+1}{2}\right)}{\Gamma\left(\frac{\nu}{2}\right)} \left(1 + \frac{x^2}{\nu} \right)^{-\frac{\nu+1}{2}}$$
f(x) = \frac{1}{\sqrt{\nu \pi}} \frac{\Gamma\left(\frac{\nu+1}{2}\right)}{\Gamma\left(\frac{\nu}{2}\right)} \left(1 + \frac{x^2}{\nu} \right)^{-\frac{\nu+1}{2}}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><msqrt><mrow><mi>ν</mi><mi>π</mi></mrow></msqrt></mrow></mfrac><mfrac><mrow><mi>Γ</mi><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mi>ν</mi><mo>+</mo><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow></mrow><mrow><mi>Γ</mi><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mfrac><mrow><mi>ν</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow></mrow></mfrac><msup><mrow><mo stretchy="true" fence="true" form="prefix">(</mo><mn>1</mn><mo>+</mo><mfrac><mrow><msup><mi>x</mi><mn>2</mn></msup></mrow><mrow><mi>ν</mi></mrow></mfrac><mo stretchy="true" fence="true" form="postfix">)</mo></mrow><mrow><mo>−</mo><mfrac><mrow><mi>ν</mi><mo>+</mo><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></msup></mrow></math>
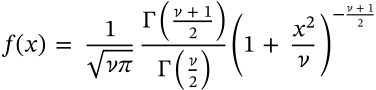
Logistic Function
logistic function
$$f(x) = \frac{L}{1 + e^{-k(x-x_0)}}$$
f(x) = \frac{L}{1 + e^{-k(x-x_0)}}
<math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mi>L</mi></mrow><mrow><mn>1</mn><mo>+</mo><msup><mi>e</mi><mrow><mo>−</mo><mi>k</mi><mo stretchy="false">(</mo><mi>x</mi><mo>−</mo><msub><mi>x</mi><mn>0</mn></msub><mo stretchy="false">)</mo></mrow></msup></mrow></mfrac></mrow></math>